CP(Copying polymath) 두 번째 문제입니다.
CP 문제는 출제자도 답을 모르는 문제이므로 폴리매스처럼 자유롭게 대화하며 비밀댓글로 정답확인요청을 하기보다는 의견을 주고받기를 원합니다. 그러므로 문제풀이에 핵심적인 아이디어를 내기만 해도 해당 소문제가 풀렸을 때 함께 부분해결로 간주하겠습니다. 또한 이 문제의 경우 2번과 3-1번까지만 풀려도 해결로 간주합니다.
일정한 공간 내에 점들이 위치하며, 임의의 두 점 사이의 거리는 1 이하일 수 없다(1도 허용하지 않는다). 공간에 들어갈 수 있는 점의 최대 개수를 구하자.
1-0.(연습문제) 반지름 1인 원 속에 (둘레 포함) 점들이 존재한다. 점의 최대 개수를 구하고 증명하라.
1-1. 반지름 2인 원 속에 (둘레 포함) 점들이 존재한다. 점의 최대 개수를 구하고 증명하라.
1-2. 임의의 반지름 r에 대해 점들의 최대 개수를 구하라. 또는 r에 대한 식을 이용하여 점들의 최대 개수가 존재할 범위를 잡아보자.
2-0. (연습문제) 반지름 1인 구 속에 점들이 존재한다. 점의 최대 개수를 구하고 증명하라.
2-1. 반지름 1인 n차원 구 (n>2) 속에 점들이 존재한다. 점의 최대 개수를 구하고 증명하라. 또한 반지름 r에 대해서도 점의 최대 개수를 생각해 보자.
3-0. (연습문제) 한 변의 길이가 2인 정사각형 속에 점들이 존재한다. 점의 최대 개수를 구하고 증명하라.
3-1. 2차원에서, 한 변의 길이가 n인 정사각형이나 정삼각형에서 (n>1) 점의 최대 개수는 어떻게 될까? 이것을 2차원의 모든 도형으로 확장할 수 있는가?
3-2. 임의의 n차원에서 임의의 도형에 대해 점의 개수를 구할 수 있는가?
4. 유클리드 공간이 아닌 공간의 경우 거리의 정의가 다른 공간들이 존재한다. 이런 공간들에서 위 문제들의 답을 생각해 보자.
좋아요
5
글쎄요
1
어려워요
1
-
다시 도전
-
우선, 원을 이용해 접근한 것이 굉장히 좋습니다. 임의의 두 점 사이의 거리가 1보다 크다고 했으므로 반지름이 1인 원을 그릴 경우 두 원이 겹치는 것은 상관없습니다. 다만 반지름 1인 원 속에 다른 점이 들어가지 않아야 합니다. 또한 원 바깥쪽에만 점이 위치할 필요는 없고 안쪽에도 위치할 수 있다는 점을 고려해야 합니다.
처음부터 저도 답을 모르는 문제이며, 함께 참여하며 풀고자 하는 문제라고 했으므로 저도 공개적으로 아이디어를 남기겠습니다.
1-1 문제의 경우 저는 답을 19로 추측하고 있었습니다. 아래 그림과 같이 배치할 경우 19개 점을, 임의의 두 점 사이의 거리가 1보다 크게 배치할 수 있습니다.
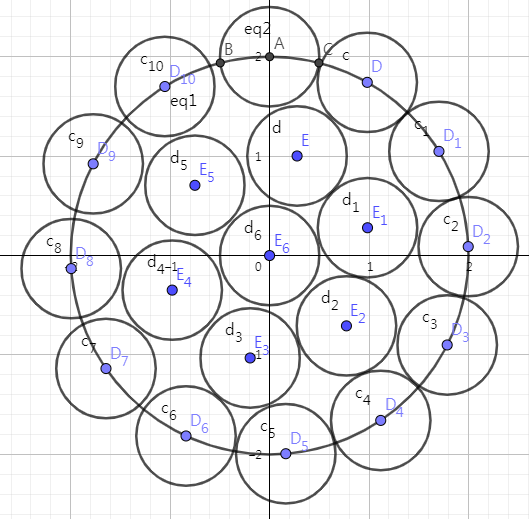
또한 힐라슨 님의 아이디어에서 각 점에 대해 그 점을 중심으로 하는 원의 반지름을 1/2라고 하면 임의의 두 원이 겹치지 않아야만 하므로 사용하신 아이디어를 그대로 다시 쓸 수 있을 듯합니다. 이 경우, 엄밀한 표현은 아니지만 바깥쪽에 점이 12개까지 들어갈 수 있을 것입니다.
좋아요0
-
-
확인요청중
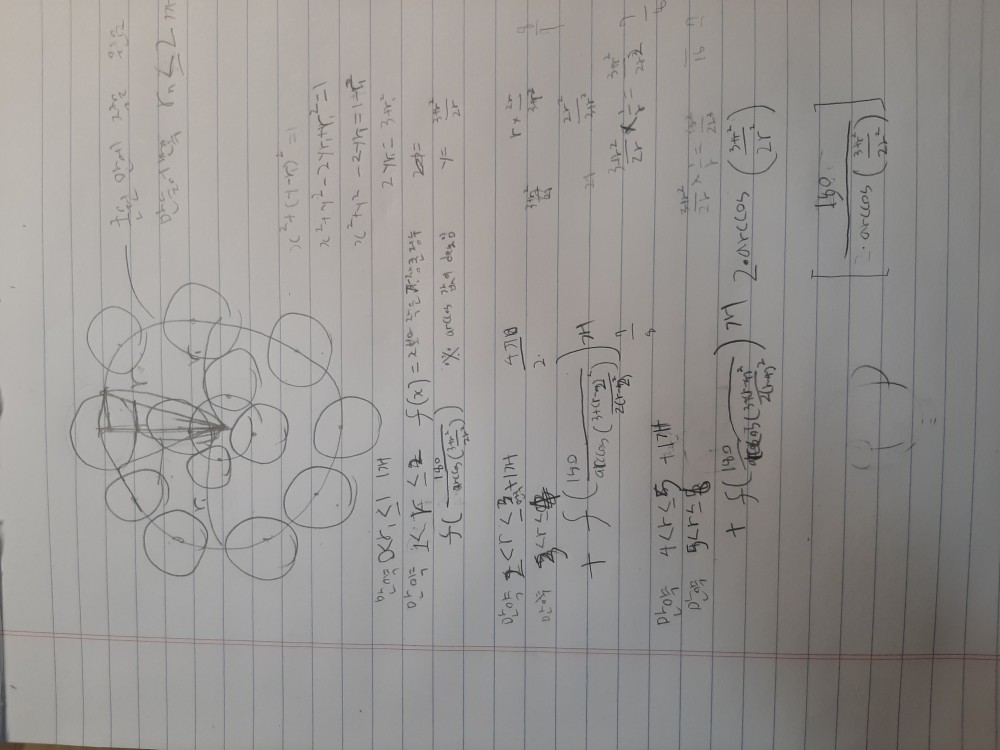 큰 원 안에작은 원 넣고 그 안에 더 작은원을 넣는방식을 반복하면 될것 같아요! 1-2 문제
큰 원 안에작은 원 넣고 그 안에 더 작은원을 넣는방식을 반복하면 될것 같아요! 1-2 문제-
풀이를 읽어보니 1-1에서 사용한 방법으로 원의 가장자리에 점을 배치한 후 안에 다시 작은 원을 만들어 같은 방법으로 가장자리를 배치하는 과정을 반복한다는 내용인 것 같습니다.
1-1에서처럼 문제에서 임의의 두 점 사이의 거리를 1 이하로 설정했으므로 반지름을 1/2로 줄여야 하는 점은 동일하고, 그 다음에 두 가지 증명해야 하는 사항이 있습니다.
먼저 저 식이 나온 과정이 분명하지 않습니다. 작은 원의 크기를 구해서 1-1의 방법을 사용하여 구한 것 같은데, 식을 유도한 방법을 좀 더 분명히 나타내 주시면 좋을 것 같습니다.
또한 밖에서 안으로 원을 넣어가며 채운다는 방식이 직관적으로는 굉장히 좋은 방법이고, 실제로 위의 1-0 문제의 해답이나 1-1 문제에서 제가 추측한 방법에서도 사용되었듯 효율이 좋은 방법이기는 합니다. 그러나 중요한 점은 '이보다 좋은 방법이 없다' 고 단정짓는 데는 증명이 필요하다는 것입니다. 만약 r이 매우 커지게 되면, 잘 알려진 '평면에 원을 채우는 문제' 로부터 바깥쪽 극히 일부분을 제외하고는 안쪽을 규칙적인 삼각형 테셀레이션 식으로 배치하는 것이 효율적일 것입니다.
힐라슨 님의 접근을 통해 대략적인 값을 추정할 수 있을 듯합니다. 이제 이 방법을 완성된 답으로 만들기 위해서, 점의 개수에 대해 상계와 하계를 잡고 그 차이를 줄여나가 추정했던 값으로 수렴시키는 과정을 거치면 1-2번의 답을 찾을 수 있을 것 같습니다.
좋아요0
-

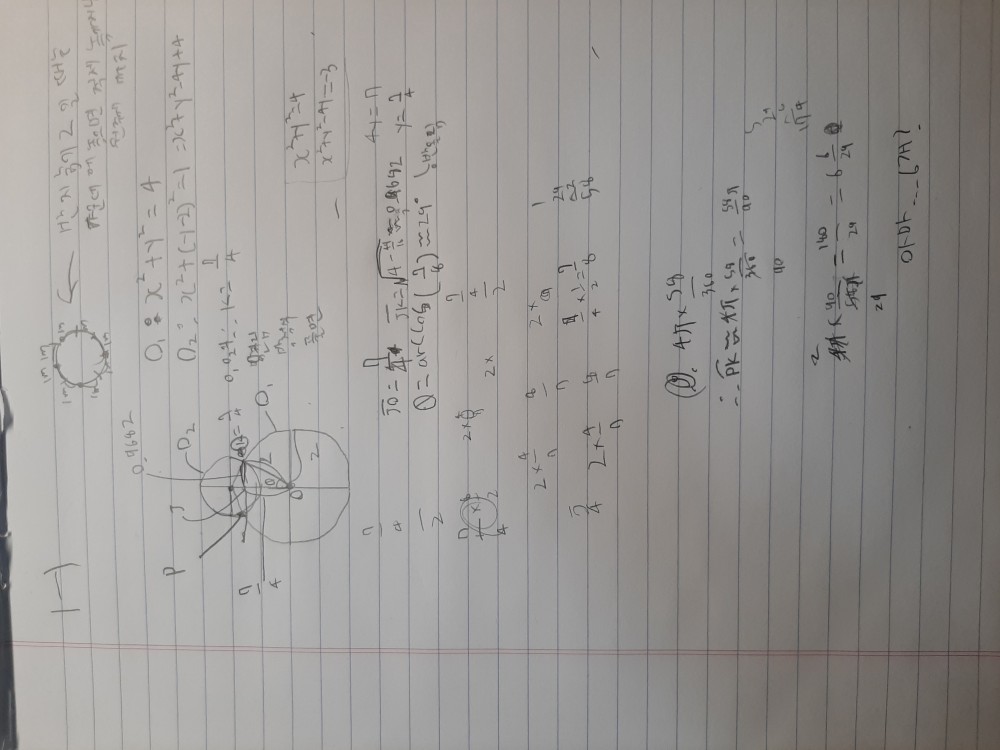 일단 1-1 풀어봤어여.. 나머진 더 자구 생각해 볼려구여 ㅎㅎ
일단 1-1 풀어봤어여.. 나머진 더 자구 생각해 볼려구여 ㅎㅎ