폴리매스

k! (k≠1) 이 완전제곱수라고 가정하겠습니다.

1부터 k번째 까지 자연수 n의 배수의 갯수는 [k/n] 입니다.

그리고 인수분해 했을 때 n은 [k/n]+[k/n^2]+...[k/n^[log_nk]] 번 곱해집니다.(이건 증명 생략 할게요..)

즉, 인수분해 했을 때 k!= 2^([k/2]+[k/2^2]+...[k/2^[log₂k]])+3^([k/3]+[k/3^2]+...[k/3^[log₃k]])+5^([k/5]+[k/5^2]+...[k/5^[log₅k]])... 이렇게 되겠죠?

그런데 k!은 완전 제곱수 이므로 ([k/2]+[k/2^2]+...[k/2^[log₂k]]) 와 ([k/3]+[k/3^2]+...[k/3^[log₃k]]) 와 ([k/5]+[k/5^2]+...[k/5^[log₅k]]).... 들은 모두 짝수여야 합니다.

일단은 시간이 없어서 여기까지만 쓸게요..ㅠㅠ

 

p!이 제곱수가 아닌 것은 자명합니다.(p는 소수)

2p!은 되어야 p²이 곱에 나타나겠죠. (p!에서 (2p-1)!은 제곱수가 아님.

임의의 정수 n에 대하여, n<p<2n을 만족하는 소수 p가 존재하기 때문에(n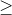2)(베르트랑 공준), p와 2p 사이에도 소수 q가 있습니다.

그리고 q!은 제곱수가 아니지요.

n=1일때는 2보다 작으므로 베르트랑 공준의 영향을 받지 않고, 그 값도 제곱수입니다.

뭐...짧게 쓰면 이건거 같은데 ㅎㅎ

자... 무슨 공식인가 정리인지는 모르겠지만 임의의 수 n과 2n사이에는 무조건 한 개의 소수가 있다는 정리. 기억하시나요?

 

자... n!=m²인 것이라고 하고 귀류법으로 증명해 봅시다~

n!에서

임의의 소수 1/2n>p>n이 있습니다. 따라서 그 p때문에 n!은 제곱수가 아닙니다. 왜냐하면 p는 소수이고, n!안에는 p를 제외한 p의 배수가 없습니다. 따라서 p의 지수는 1입니다

->제곱수가 아닙니다.