함께 풀고 싶은 문제
창의력을 기를 수 있는 수학 문제 또는 퍼즐을 내는 곳입니다.
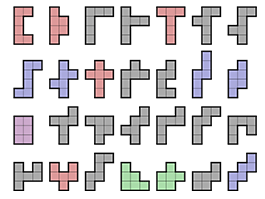
폴리오미노란 크기가 같은 정사각형 n개가 변끼리 이어붙여 만든 도형이다. 물론 꼭짓점끼리만 만나는 것은 폴리오미노가 아니다. 정사각형 개수에 따라 모노미노(1개), 도미노(2개), 트로미노(3개), 테트로미노(4개), 펜토미노(5개), 헥소미노(6개), 헵토미노(7개)... 로 나뉘어진다. 여기서 모노미노와 도미노를 제외하면 한 종류의 블록을 모두 1개씩만 써서(예를 들어 테트로미노를 모두 1개씩만 사용하여) 이어붙여서 직사각형을 만들 수 있는 도형은 펜토미노밖에 없다. 그것을 증명해 보아라. 단, 이어붙일 때 겹치는 부분이 있으면 안 되고, 뒤집거나 돌려서 같은 모양은 같은 모양으로 본다.
이 문제 어떠셨나요?
좋아요
0
글쎄요
0
어려워요
0
댓글 4
댓글 작성하기
-
트로미노는 길게 3개가 붙은 것과 ㄱ자 모양 뿐이어서 직사각형을 만들 수 없고, 헵토미노 이상부터는 고리 모양이 가능하므로 중간에 빈 공간이 생깁니다. 아래에 부가 이미지 넣겠습니다.
-
트로미노에 대해 부가 설명을 하자면, 트로미노는 2가지로 2*3 혹은 1*6 두 가지 직사각형을 만들어야 합니다. 그런데 두 가지 모두 긴 모양을 채우고 나면 같은 긴 모양밖에 남지 않으므로 불가능합니다.
좋아요0 -
"항구" 펩토미노입니다. 가운데 구멍이 비어 있어 면을 완전히 채울 수 없게 합니다.
출처:https://librewiki.net/wiki/%ED%8F%B4%EB%A6%AC%EC%98%A4%EB%AF%B8%EB%85%B8
좋아요0 -
네, 이제 테트로미노와 헥소미노만 증명을 하면 되겠습니다. (단, 그게 난이도 상입니다.)
좋아요0
-
닫기
