함께 풀고 싶은 문제
깊이 고민해볼 수 있는 수학 문제를 내는 곳입니다
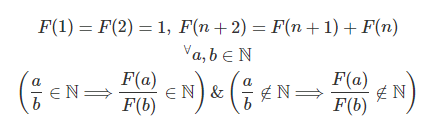
피보나치 수열(Fibonacci sequence)은 아래와 같은 점화식으로 정의되는 수열이다. (피보나치 수열의 n번째 항을 F(n)이라 정의하자)
F(1) = F(2) = 1, F(n+2) = F(n+1) = F(n)
이 피보나치 수열의 항을 앞에서부터 나열해보자면 아래와 같다.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...
이때 어떤 자연수 a, b에 대해 다음 사실이 성립함을 증명하시오
a가 b의 배수이면 F(a)도 F(b)의 배수이다.
a가 b의 배수가 아니면 F(a)도 F(b)의 배수가 아니다.
이 문제 어떠셨나요?
좋아요
0
글쎄요
2
어려워요
0
닫기