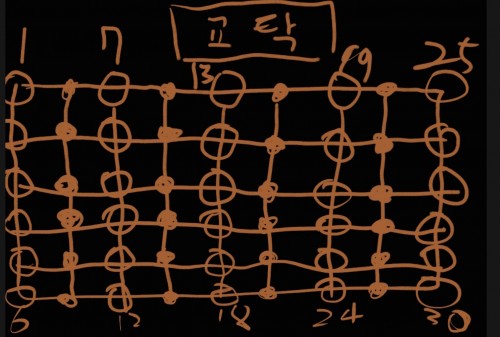
인터뷰하니 기억나는데,원래 이 문제도 자랑하고 싶었지만 당시 답을 하나도 모르는 상황이라 올리지 못한 문제입니다. 당시는 계산을 안해서 모르겨,지금은 더 작은 수가 나올까봐 아직 확신이 안서는 문제입니다. 인터뷰 내용에 있는 자리 이동 문제가 바로 이겁니다.
(그리고 당연히 모눈 1칸 움직이는게 1번이다)
1번. 자리는 저 방식대로 순서대로 구성되어 있다. 빈칸 동그라미는 책상,점은 빈 곳이다. 여기서 4번 줄과 5번 줄의 위치를 바꿀 때(줄에서의 번호 순서는 일정하게-1~6,7~12...),가장 적은 수로 책상을 움직여서 위치를 바꾸어라.(몇회인지 구하기-얘만)
2번. 가운데 3줄은 순서를 상관없게 하되,1번 줄과 5번 줄의 위치를 최소의 움직임으로 바꾸어라. 단 줄별 순서는 위 문제와 같이 유지하도록 하게 한다.
3번. 자리의 순서를 좌우반전으로 최소한 움직여 바꾸어라(1번줄은 25~30,2번 줄은 19~24...).
4번.상하좌우 대칭으로 최소한으로 움직여 바꾸어라.
5번. 우리 반은 5번 줄이 6개가 아닌 4개이다. 이때 1~4와 같은 원리로 시행하는,최소로 움직이는 경우의 수들을 구하여라.
6. 한번에 1개씩이 아닌 인접한 2개씩 움직이게 할 수 있다면,가능할까?(단,2개씩 움직여 1~5번과 같은 식으로 하는 것입니다.)
7. 그렇다면,위 문제들이 가능할 때,바꾸는 경우의 수를 구하라(예시로 1번에서 바꿀수 있는 최소 경우의 횟수뿐만이 아닌,그 수로 바꿀 수 있는 모든 경우의 수를 구하는 것).
(1,2,3,4번은 2개당 해결인데,5번은 소문제 속 소문제 2개만 해결해도 해결 드릴 정도로 난이도가 달라집니다. -당연히 출제자는 5번 답을 모른다. 1개 빼고-)
모든 문제는 불가능이 생길 수 있으나,그러면 그걸 증명하면 된다.
좋아요
2
글쎄요
0
어려워요
0
-
-
-
-
문장제 문제가 아니라요? (이게 세상을 바꾸는 이유: 일상 속 문제를 수학적으로 접근해서,세상에 도움이 된다. 적어도 저의 의견은요)
창의 퍼즐은 규칙을 찾는 건데...
좋아요0 -
저는 창의 퍼즐이 꼭 규칙을 찾는 문제라기보다는 퍼즐 형태의 문제가 모두 포함된다고 생각하고, 그런 점에서 이 문제는 창의 퍼즐에 더 어울린다고 판단했습니다.
일단 문장제 문제는 아닌 것 같습니다.
좋아요0 -
흠...리퍼님은 세바문의 기준이 무엇이라 생각하나요?
(분명 이것보다 더한것도 본 것 같다 생각하였고,또한 요즘엔 기준이 너무 명확하지 않은 상황임을 아실 겁니다.)
좋아요0 -
예전부터 세상을 바꿀 문제의 구분이 명확하지 않긴 했습니다. 예전에 이 주제로 토론이 이루어진 적도 있고요.
전 창의퍼즐은 말 그대로 퍼즐 문제가 해당된다고 생각합니다. 이 문제도 퍼즐 형태에 가깝다고 생각했고, 실제로 비슷한 유형의 퍼즐 문제가 꽤 있습니다.
아래는 제가 가장 이상적이라고 생각하는 세상을 바꿀 문제입니다. 단순 개념으로만 푸는 것이 아니지만 퍼즐 문제는 아닌 것들이죠.
http://www.polymath.co.kr/contents/view/26278?page=3
http://www.polymath.co.kr/contents/view/19236?page=3
좋아요0
-
-












