오늘 학교 수업시간에 갑자기 떠오른 엄청난 방법입니다.
혹시 (세 자리 수) * (두 자리 수) 또는 (n 자리 수) * (a 자리 수) 곱셈 하시는 분 있나요?
저는 현재 4학년이라서 (세 자리 수) * (몇십) 을 하고 있는데요, 여기에 엄청난 계산법이 있다는 것을 알고 계시나요?
예제: 392*38을 계산하라.
이 문제에 답을 구하는 방법이 있습니다.
일단, 어림을 해야 하는데요,
여기서 계산을 쉽게 하려면, 정확하지 않더라도 더 작게 어림하는 것이 중요합니다.
또, 앞 자리의 수 (곱해주는 수)는 어림하면 안됩니다.
즉, 367*50의 경우, 367을 300이라고 어림하는 것이 좋습니다.
그럼 원래 문제는 300*38로 어림할 수 있는데요, 이것을 계산하면 일단 0을 모두 빼고, 그 결과(38*3)을 계산합니다. 그럼 이 결과는 114가 됩니다.
이제 0을 다시 추가해서 11400으로 만들 수 있습니다.
그럼 이제 원래의 방법으로 세로셈을 좀 해야 합니다.
그. 래. 서!
세로셈 하는 중입니다...
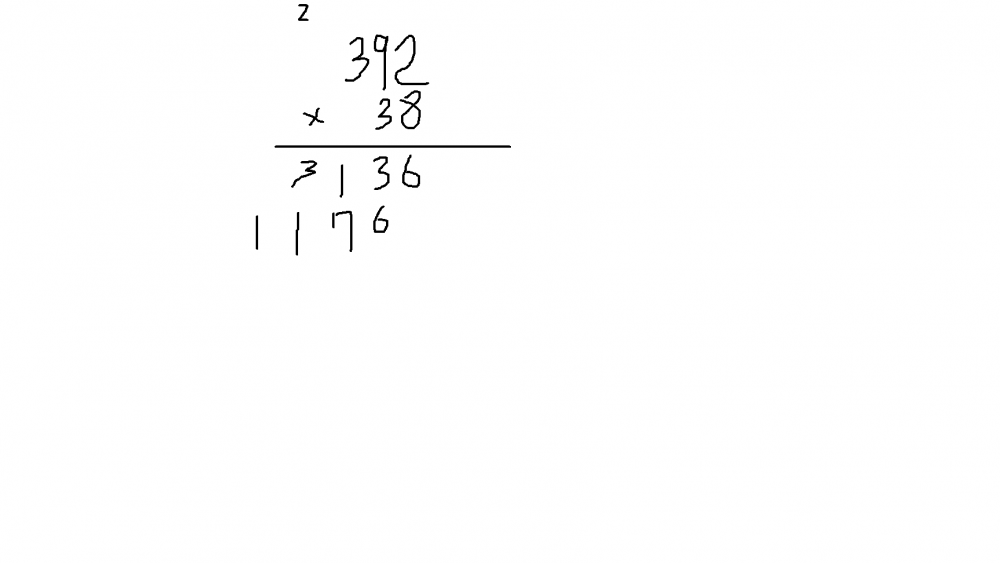
아니 왜 내 말로 쉬운 방법이 있다면서 계산기로 검사를 하니 어이구 ㅠㅠㅠ
암튼 저 곱셈의 답은 14896입니다.
그럼, 이제 검사를 한번 해볼게요.
1. 원래 곱셈의 답에서 어림한 값에 답을 뺍니다. (14896-11400=3496)
2. 이제 오류 확인을 해야 하는데요, 나눗셈식으로 확인을 할 수 있습니다.
3. 나눗셈식은 (곱셈 답-어림한 수)/(곱해주는 수) 로 세워야 합니다.
4. 그럼 계산해 봅시다.
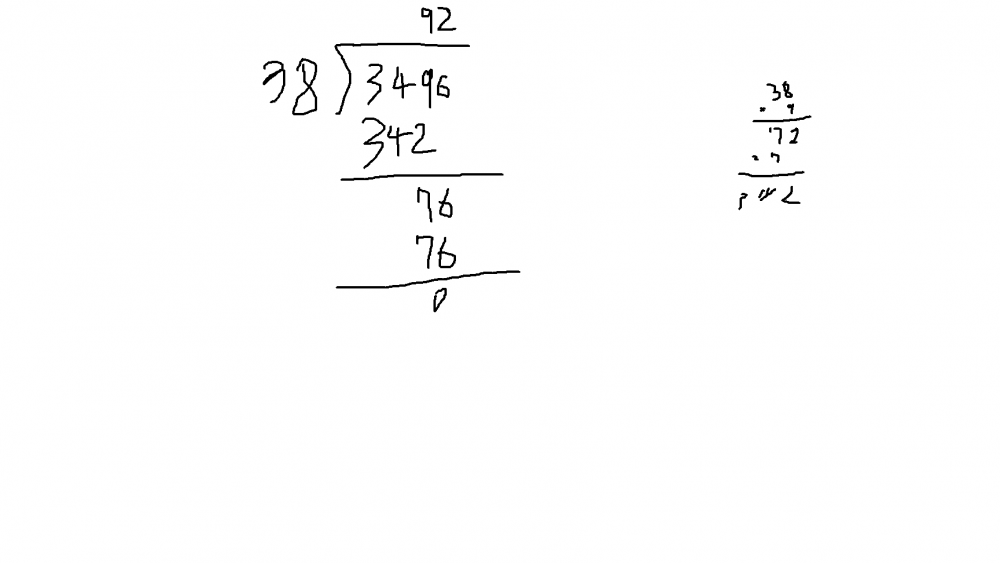검증 방법:
(곱해지는 수)-(곱해지는 수를 어림한 수)가 나눗셈식의 몫이고, 나눗셈식의 나머지가 0이면 맞게 계산한 것입니다.
이렇게 곱셈을 검증하는 방법을 알아봤습니다.
