폴리매스

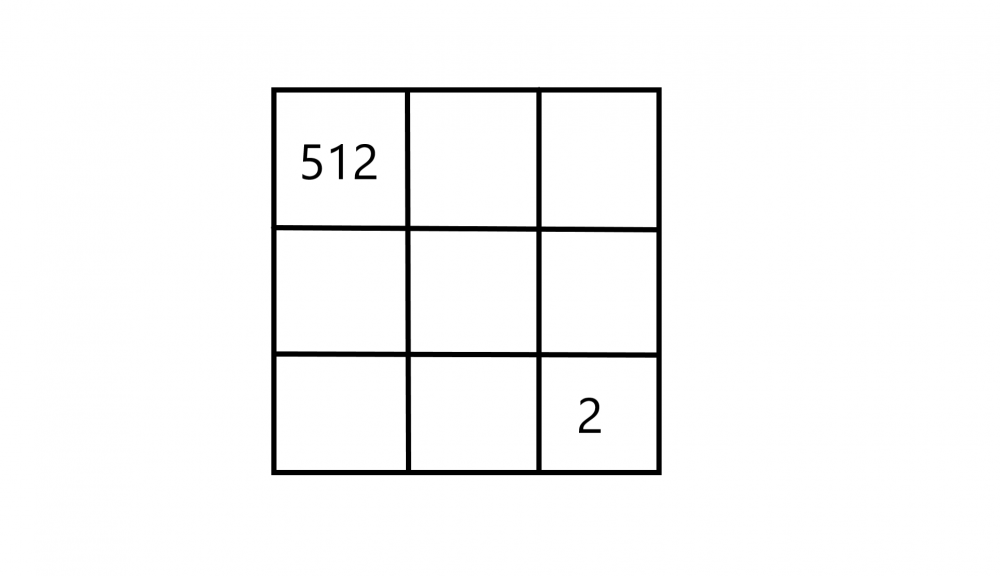
연련은 좌측 상단에서부터 2^9의 자리부터 지수를 1씩 줄이도록 한 자리수에 대한 이진등(1의 값을 소유할 시에만 켜짐)이 위치해 있다. 각 이진등은 규격이

모두 동일하며 정사각형 형상을 띈다. 전 등의 각도는 90n(n은 임의의 양의 정수)도로 무작위 설정되어지며 등 외에는 빛의 유입량이 전무하여 등 전반의 형체를 인지 불가하다 가정한다.

이 때, 점등된 등에 해당하는 값의 경우당 합의 평균이 13번째로 큰 형태들 내에서 켜진 등에 해당하는 값의 합 중 가장 큰 수와 두번째로 큰 수를 모두 구하여라.

일례로 

위와 동일한 형상 내에서 켜진 등에 해당하는 2의 거듭제곱을 합산한 가장 큰 값는 2⁹+2⁸+2⁵+2³=808, 두번째로 큰 값는 2⁹+2⁷+2⁵+2⁴=688입니다. 

혹시 위 문제를 이해 불가하실 경우 비밀댓글로 문의하셔도 물론 무방합니다.