함께 풀고 싶은 문제
창의력을 기를 수 있는 수학 문제 또는 퍼즐을 내는 곳입니다.

여러분 모두 하노이탑에 대해서 들어봤을 것이다.
이 하노이탑은 원판 여러개를 가지고, 강증가의 형태로 원판을 쌓는 것이다.
이때, 라임은 문제를 살짝 바꾸어서, 다른 문제로 바꾸어보려 한다.
원판은 어떻게 놓든 상관이 없다.
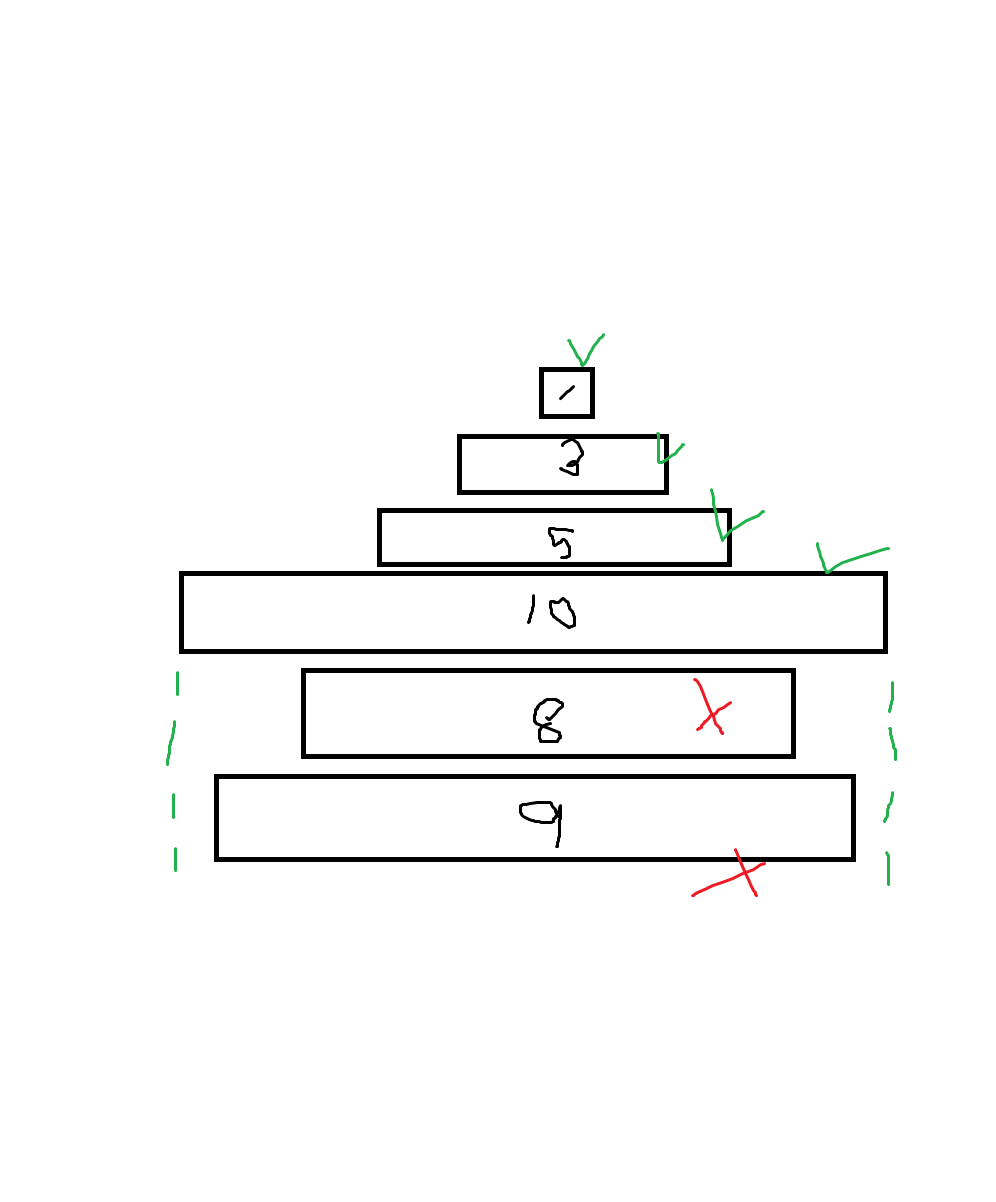
다만, 위에서 보았을 때, 특정한 개수만큼의 원판이 보여야 한다.
(원판이 보인다는 것은 수직 위에서 내려다 보았을 때 원판이 조금이라도 형체가 확인 가능할 때이다.)
이때, 다음 물음에 답하여라.
1) 색과 크기가 모두 다른 원판 7개를 배열한 후, 위에서 보았을 때 원판이 3개가 보이는 경우는 몇 가지인가?
2) 색은 모두 다르나, 크기가 같은 원판 한 쌍이 존재하는 원판 7개를 배열한 후, 위에서 보았을때 원판이 2개가 보이는 경우는 몇 가지인가?
[풀이 필수, 소문제당 해결 하나]
이 문제 어떠셨나요?
좋아요
2
글쎄요
0
어려워요
0
닫기