폴리매스

근데 제가 알기론 정답을 올릴거면 비밀댓글로 해야할텐데..

저 어제 시작해서 이거 풀 땐 몰랐어요. 죄송합니다.

그렇게 따지자면 한도 끝도 없죠...

1부터 100000까지 다 더해라!

우선, 1부터 2까지 더하는 것은 3이다. 하지만 이는 2+1을 다시 하면서 2로 나누면 3*2/2=3이다!

...

이와 같이 하면, 1부터 100000까지 더하고, 다시 100000부터 1까지 더한 걸 다시 더해봅시다. 그러면 100001*100000/2=5000050000입니다!

아니죠! 이는 그저 작은 수에 대해서 대입한 것일 뿐, 100000에 대해서 성립할 거라는 보장이 어딨습니까?

그러므로 1부터 2까지, 1부터 3까지, 1부터 4까지... 1부터 12까지...1부터 1832까지...1부터 62846까지... 1부터 100000까지!!

다 해보지 않는 이상 이 문제를 단순문제라고 할 수 있을까요?

정확한 풀이로 다시 해오세요!

이런 논리와 같다고 생각합니다.

1부터 100000까지 더하는건 논리적으로 풀이를 간추릴 수 있습니다.

1+2+3+4+ ... + 99997+99998+99999+100000

10000 +99999+99998+99997 + ... +4+3+2+1

이렇게 두 번 쓰면, 윗줄에서 i번째 수는 i, 아랫 줄에서 i번째 수는 100001-i가 되죠.

그러면, 윗줄과 아랫줄을 한 번씩 더해서 결과를 써보면, 총 수의 개수 100000에 i가 1~100000일때 합이 항상 100001이 되므로 100000*100001이 됩니다.

또, 모든 수가 두 번씩 쓰였으므로 2로 나눠주면 되죠.

이런 문제는 가우스에 대한 이야기로도 많이 알려져있고, 그 방법대로 논리적인 전개를 통해 짧은 풀이로 풀 수 있습니다.

여기 풀이 쓰라고 해서 제가 그렇게 풀었는데요?

@원형파이

그렇게 따지자면 이 문제도 한 줄로 간추릴 수 있죠!

임의의 352 미만의 자연수 x에 대해, x번째 사람이 당첨되지 않을 확률은 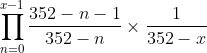로 나타낼 수 있으니까요

이 공식에서 352만 다른 수로 치환하면 아까 말씀하신 가우스의 사례가 되는 겁니다.

사실 위에 쓴 말도 수학동아님께서 쓰신 말을 간추린 거죠

그렇기에 제가 이 문제를 단순문제로 판단한 이유고요!

죄송하지만 제가 중3을 하고 있어서 그 식을 모르겠네요.

@수학동아 아, 당신께 말한 게 아니었어요.

원형파이님께 말씀드린 겁니다.

@삼각파이

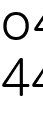 이 식에 수를 대입해서 푼다면 문제가 되겠지요.

그러나 이 공식을 증명하는 과정이 풀이에 포함되어 있다면 풀이에서 마음껏 사용해도 괜찮지 않을까요?

자기가 풀이를 짧게 간략하게 적기 위해서 공식을 만들고, 이를 증명한 후에 쓴다면 괜찮을 것 같습니다.

가우스의 사례는 1부터 10만까지, 10만부터 1까지 순서대로 적고 세로의 합을 구함으로써 증명을 포함한 풀이가 됩니다.

@원형파이

공식 하나로 쉽게 풀리는 문제라면, 단순문제라고 칭해야 한다고 생각합니다.

애초에 공식으로 칭하는 것이 복잡하지, 저 문제는 확률을 조금만 공부한 사람이라도 누구나 풀 수 있는 문제니까요.

저 가우스의 사례와 다를 게 없다고 생각합니다.

@삼각파이

1부터 n까지의 합 문제는 유명하고 잘 알려진 공식으로 풀 수 있습니다.

'마인크래프트 세상에서 22학교 강당에서 학생352명이 제비뽑기를 해서 종이352개중에 o가 적힌 종이 한장을 뽑으면그 학교 전체의 반장이 된다고할때 x번째로 뽑을때 반장이되는확률', 조금 간단히 하고 일반화를 하면 'n명이 n개 종이 중 하나의 o를 뽑으면 대표가 될때 x번째로 종이를 뽑을때 대표가 될 확률' 에 대한 공식이 잘 알려져 있나요?

아니요, 저는 단한번도 본 적이 없습니다.

문제에 주어지는 n에 따라 공식을 만들어야겠죠.

공식을 풀이 내에서 만들거나, 혹은 증명 한 후에 사용하는 것은 '공식 하나로 쉽게 풀린다'고 할 수 없다고 생각합니다.

그냥 공식을 구글링 혹은 이미 알고 있는 지식으로 알아내어 숫자를 때려넣은 후에 답을 내는 것은 정확한 풀이가 아닙니다.

자신이 증명하지도 못하는 공식을 자신이 써서 문제를 푼다니요? 이건 말이 안되죠.

또, 대댓글이 달리는 본 댓글에서 언급했다시피, 확률을 조금 공부한 사람이라도 누구나 풀 수 있는것은 분명한 사실입니다.

'351/352x350/352x349/350x...x352-n/353-nx1/352-n'  이런 식을 계산해서 풀면 되니까요.

저는 이러한 이유로 1부터 n까지의 합 문제와 차이가 있다고 생각합니다.

@원형파이

실제로 저 공식 없이도 풀 수 있는 문제입니다.

굳이 그 공식을 만들 필요조차도 없고요.

그냥 간단한 확률 계산만 하면 되는 문제입니다.

어... 정말 무례하고 죄송한 말씀이지만

제가 지금까지 반박하고 있던 의견은 '이런 작은 수의 예시들이 그 다음에도 성립할지 누가 아냐, 고로 이건 더 생각해봐야 하는 문제고, 단순문제가 아니다'라는 의견입니다.

이 문장은 제 관점에서 봤을 때는 조금 억지라고 느껴집니다.

작은 수의 예시들이 다음에도 성립할지 누가 알까요? 왜냐? 모두가 압니다. 왜나? 자명하기 때문이죠.

다음 경우로 갈 수록 분자가 하나씩 줄어들고 분모가 하나씩 줄어들며 최종 분자는 1이기에 모두 약분되어 1/352가 나올 수밖에 없죠.

그래서 첫 반틈의 문장은 억지라고 해석될 요지가 있습니다.

두 번째 반틈에 대해서...

이 문제는 중2 '경우의 수와 확률' 단원에서 확률을 공부하게 되면 '기본 문제'로 나오는 문제입니다.

다시 말해, 확률 개념을 알기만 하면 풀 수 있는 문제라는 겁니다.

그 문제의 정의는 우리가 이미 알고 있습니다. 단순문제죠.

마블이님께는 정말 죄송하지만, 이 문제는 단순문제로 판단될 소지가 있음을 말씀드리고 싶었습니다.

한 사람의 견해일 뿐이니 너무 상처받지는 말아주셨으면 좋겠습니다.

앞으로 좋은 문제 기대할게요!