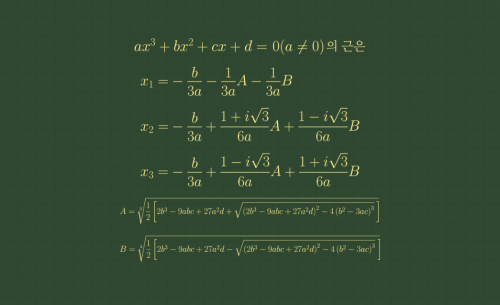폴리매스

왜 단순문제라고 생각하시는지 궁금하네요. 단순문제라고 생각되면 직접 풀어보십시오. 또, 다른 어려운 문제를 풀어보고 싶다면 찾아서 푸시죠. 저는 개념응용이라고 올렸습니다. 개인적인 의견으로 부탁해주시는 것은 삼가해주시고, 온라인상에서도 예의를 지켜주셨으면 좋겠습니다.

예의를 지키는것이 아니라 단순문제를 보면 적발하는 것은 당연한 것입니다

이런 문제는 시도때도 없이 쉽게 내고도, 풀 수도 있습니다

여기서 말하는 단순문제는 단순문제이기도 하지만 성의없는 문제이기도 합니다

궁금하시면 이걸 읽어보시는것도 좋습니다 http://www.polymath.co.kr/contents/view/25621

그리고 이 문제를 한번 풀어보겠습니다

각 블록마다 1칸 간격으로 놓는다 입니다

너무 쉽지 않습니까?

이러한 단순문제를 내는 행위는 그만하셨으면 좋겠습니다

그리고 이 문제를 실제로 성의를 들여서 내신 문제입니까?

그리고 온라인상에서의 예의는 마블이 님이 지켜주셨으면 감사하겠습니다

개념응용이면 일정한 주제의 개념을 가지고 그것을 응용해서 내는 문제입니다

그런데 이것은 제 동생도 풀 수 있을 만큼 쉬운 문제입니다

다른 어려운 문제를 풀어보고 싶다면 찾아서 푸시죠 라는 말에서 저는 예의가 올바르지 않다는 점을 알았습니다

먼저, 수락 님의 풀이는 틀렸습니다. 단순 문제라고 생각하실 자격이 없으시군요. 수락 님은 1칸당 하나씩 놓는다고 하셨는데 모든 블록이 모두 같은 거리만큼 떨어져 있어야 하므로 답에 0.1% 도 가깝지 않습니다. 물론 정다각형 모양으로 배치한다 또는 모든 블록을 붙여서 놓는다 등도 대각선 등의 이유 때문에 틀렸습니다.

수락 님이 아무리 어려운 문제를 많이 풀어 보셨어도 정답도 아니면서 풀 가치도 없다고 하시니 안타까울 다름입니다. 다시한번 예의를 지켜주시기 바랍니다. 또, 다른 어려운 문제를 풀어보고 싶다면 찾아서 푸시죠 란 말은 이런 문제를 풀고싶지 않다는 줄 알고 권해드린 것이지 절대로 예의를 지키지 않지는 않았습니다.

마블이 님이 말씀하신것은 맞긴 합니다

하지만 예의상의 문제로는 마블이님이 더 심각하고 

무엇보다성의가 없다는 것이 문제입니다

제가 말했던 위 링크를 들어가 보시면 이해가 되실거고 보시면 글 삭제 부탁드립니다

그리고 문제도 충분한 조건이 추가되어있지 않습니다

자격이 없다는것도 심각한 예의문제입니다

위 링크를 보시면 다 이해가 되실테니 꼭 글 삭제 부탁드립니다

아니면 잡담에 이것에 대한 글을 올리겠습니다

문제의 답은 여러가지가 될 수 있으므로 추가적인 말은 안하겠습니다

먼저, 제가 예의를 지키지 않았다는 수락님의 언급에 대해서는 인정합니다. 하지만 저는 이 문제를 충분한 조건이 주어지도록 제시하였고, 답 또한 한가지만 나올 수 있습니다. 수락님이 그렇게 생각하신다면 한번 답을 말씀해 주십시오. 또, 저 또한 수락님에게 정중하게 수락님의 댓글을 삭제 부탁드리겠습니다. 문제는 성의가 없지 않습니다. 단지 수락님이 풀지 못할 뿐 이지요. 위 링크를 보았습니다. 제 문제는 그 문제처럼 전혀 단순하지 않고, 상상이 필요한 문제입니다. 단순한 계산문제가 아니란 말입니다. 수락님은 무엇보다 문제도 풀지 못하시면서 단순문제라고 하시는 것이 수락님의 단점이라고 생각합니다.

또 추가적으로 말씀드리자면, 아인슈타인 님은 매우 논리적이고, 타당한 근거를 제시하며 단순문제라고 반박했지만, 수락님은 젼혀 근거도 제시하지 않고 단순문제라고 하셨을 뿐만 아니라 수락님은 풀지 못하시는 문제를 수락님의 실력 탓으로 돌리지 않고, 문제 탓으로 돌리고 있습니다. 제발 이런 행위 멈추어 주십시오.

위 글을 제대로 못읽으신것같은데

어떤 사람에게는 어려울 수는 있다고 나옵니다

하지만 어떤 한 사람에게 특정하게 어렵다고 단순문제는 아닙니다

저는 정확하게 말하자면 이 문제가 단순문제라고 생각하진 않습니다

마블이님의 말을 들어보니 단순문제는 아닙니다

하지만 성의가 보이지 않습니다

이 문제가 성의가 보이지 않다는것은 아인수타인님도 옛날에 매스파이님에게 말했던 말입니다

타당한 근거는 말이죠

그럼 먼저 이 문제에 성의가 있다는 것을 보여주십시오

그리고 제가 이 문제가 어렵다고 해서 성의가 없는 문제라고 단정짓지는 않습니다

단지 이 문제에 성의가 보이지 않다는것입니다\

만약 이 문제를 삭제하시기 싫다면 최소한의 스토리라도 넣어서 수정해주시면

최소한의 성의라도 보일테니 성의를 넣어서 수정해주세요

그리고 이 문제의 답은 당연히 정사면체 모양으로 놓는 것이겠죠?

근데 3차원 격자블록을 가지고 배열하는거기 때문에 .... 단순히 정사면체가 아닐수도 있습니다.

만약에 문제에서 말하는 블록사이의 거리가 블록사이점의 최소거리를 말하는거이면 답이 없거나, 꽤 어려운 문제가 될듯 합니다.

그런 경우에는 답이 없을 확률이 높죠

이거 답 존재하고 이게 단순문제라고 보진 못할 것 같아요.

제 생각에는 답이 꽤 창의적이라고 생각됩니다

왜냐하면 단지 문제의 길이가 짧다고 해서 성의가 없는 문제처럼 느끼신다면 제 문제들 중에서 한줄인 문제가 꽤 있는데 그 문제들을 한번 풀어보시고 말씀해주세요.

만약 문제 길이가 아닌 어느 부분에서 단순 문제라고 느끼셨다면 말씀해주세요

(그리고 처음 문제 내신 분인데 단순문제에 대해서 설명해주시고 이러이러해서 단순문제이다! 라고 말씀해주시면 좋을 것 같아요)

만약 일단 이 문제까지는 단순문제(성의업는문제) 가 아니라고 지정하면

다음 확률 문제는 사실 기본개념으로 풀 수 있는 문제이지 않습니까?

사람들 말을 들어보니 이 문제까지는 허용할 수 있다만

확률문제는 어떻게 생각하십니까?

만약 '이 문제까지는 허용할 수 있다'면 이 문제에서는 그만 얘기 해주시는건 어떨까요.

이 문제는 '마인크래프트'라는 문제이지, '확률과 제비뽑기' 문제가 아닙니다.

여기 이 문제에서 출제자분이 '확률과 제비뽑기' 문제에 대해 이야기해야 할 이유가 무엇이 있을까요?

해당하는 문제이지 않을뿐더러, 수락님은 아무런 이유 없이 단순문제라고 판단하셨습니다.

그러나 수락님은 '이 문제까지는 허용할 수 있다만' 이라고, 출제자분께 근거없는 말을 한 것에 대해 이 한마디로 얘기를 끝내셨습니다.

과연 출제자분은 기분이 어떨까요? 상대방을 존중해주시면 좋을 것 같습니다.

아 네 그래서 이제 여기서는 나가는게 좋겠군요

그리고 문제를 낼때는 너무 짧게 내면 그러니까 스토리나 정확한 규정을 알려주십시오

그러면 저는 확률 문제로 가겠습니다

그렇죠. 이 문제는 모순이기만 합니다.

정사면체 만들면 된다는거 누가 모르겠습니까(수락님 빼고)

그런데 마크세상에는 안됩니다.

고로 이 문제는 엉망입니다.

'현실에서 구슬 4개를 모두의 길이가 똑같게 놓아라' 라는 문제가 더 정확할 것 같네요.

그러네요... ㅋㅋ 다들 수학 너무 잘하시는데여? ㅋㅋㅋㅋㅋ

@마블이