23번째 문제는
KPP 멤버 '안진후' 님이 만든 문제입니다
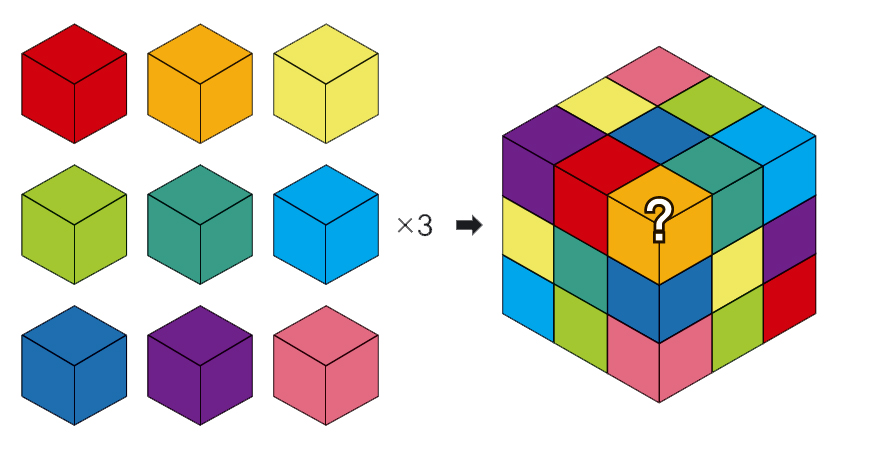
서로 다른 9가지 색을 가진 정육면체가 각각 3개씩 총 27개 있다. 이 정육면체들을 3×3×3 정육면체로 쌓되, 각 면마다 9가지 색이 모두 보이게 만들 수 있을까? 가능하면 예시를 찾고 불가능하다면 증명하라.
★주의 사항★
정답과 풀이는 비밀 댓글로 부탁드려요!
이름, 주소, 연락처를 함께 남겨주세요!
당첨자는 수학동아 12월호에 공개합니다!
풀이는 11월 25일 이후 이 게시물에서 확인하세요!
*KPP (Korean Puzzle Party)는 '퍼즐을 좋아하는 사람들의 모임'으로 퍼즐을 모으는 사람, 퍼즐을 만드는 사람, 퍼즐을 푸는 사람들이 모여 직접 만들고 수집한 퍼즐을 함께 풀어보며 이야기를 나눈다. 현재 두 달에 한 번 서울에서 정기적인 모임을 갖고 있으며, 퍼즐을 푸는 것뿐 아니라 퍼즐 관련 행사에 참여하거나 박물관에 다녀오는 등 다양한 활동을 하고 있다.
스크롤 주의!
아래 정답이 있습니다!
.
.
.
.
정답과 해설
가능하다!
3×3×3 정육면체에서 각 면의 중앙에 있는 조각을 센터, 모서리 중간에 있는 조각을 엣지, 그리고 꼭짓점에 위치한 조각을 코너라고 부르자. 27개의 정육면체는 6개의 센터, 12개의 엣지, 8개의 코너, 그리고 숨어있는 정중앙 조각 1개로 이루어진다. 각 조각마다 밖에서 보이는 면의 수를 세면 다음과 같다.
| 숨은 조각 | 센터 | 엣지 | 코너 |
| 0 | 1 | 2 | 3 |
각 색 큐브는 보이는 면의 합이 6이어야한다는 사실을 염두한 뒤 아래 과정을 쫓아가자.
① 정중앙에 숨는 큐브의 색을 A라고 하자. 남은 두 큐브의 면 수의 합이 6이 돼야하므로 A의 남은 두 조각은 모두 코너다.
② 다른 색의 큐브들은 코너를 2개 이상 가질 수 없다. 따라서 남은 여섯 개의 코너는 모두 다른 색이어야 한다. 순서대로 BCDEFG라고 하자. 코너 하나가 세 면을 차지하므로 남은 셋을 채우려면 두 조각 중 하나는 센터, 다른 하나는 엣지가 돼야 한다. 고로 '센터-엣지-코너' 조합이 6개 생긴다.
③ 남은 조각은 엣지 뿐이므로 '엣지-엣지-엣지' 조합이 2개 생긴다. 이들 색은 H, I로 지칭하자.
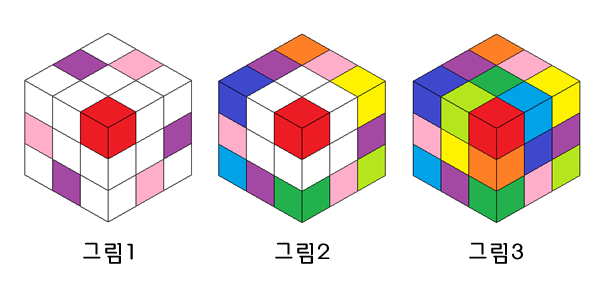
주어진 조합들을 배치하는 가장 간단한 방법은 범대각선_두 마주보는 꼭짓점을 이은 대각선_을 축으로 삼고 회전 대칭을 고려해 놓는 것이다.
이제 A 큐브를 범대각선에 나란히 배치하고 A 큐브와 닿지 않는 엣지들에 H와 I를 번갈아 배치한다(그림1). 남은 코너마다 B부터 G까지 넣고(그림2), 각 색마다 코너가 차지한 면을 제외한 다른 세 면에서 센터와 엣지 하나씩 선택하여 집어넣으면 된다(그림3).
조건을 만족하는 배치는 소개된 것 이외에도 더 있을 수 있다.
-끝-













