
KPP와 함께하는
퍼즐라이프
퍼즐러가 사는 법
퍼즐을 좋아하는 사람들이 모인 단체
KPP_Korean Puzzle Party 멤버들이
매달 재밌고 유익한 퍼즐 이야기를 들려드립니다.
KPP와 함께 신기한 퍼즐을 살펴보고
그 속에 숨은 수학도 즐겨보세요!
*사진 출처: 김우현
--------------------------------
오늘은 위상수학의 한 분야인
‘매듭 이론’과 관련된 '클로버 퍼즐'을 소개할게요.
우리가 흔히 알고 있는 매듭과 수학에서 말하는 매듭은
어떤 차이가 있는지 살펴보고
클로버 퍼즐의 해법을 분석해보도록 해요!
1
극악의 난이도를 가진 클로버 퍼즐
클로버 퍼즐은 중국의 퍼즐 디자이너
아론 왕_aaron wang이 만든 퍼즐로
왕이 만든 퍼즐 중 난이도가 매우 어려운
축에 속합니다.
겉모습을 살펴보면
세잎클로버 장식이 달린 목걸이의 끈을
반지 모양 고리에 통과시킨 뒤
그 고리가 빠지지 않도록
한쪽 끝에 커다란 나무 공을 매달아 놓은
모습입니다.
클로버 퍼즐의 목표는 바로 이 고리를
목걸이로부터 분리하는 겁니다.
절대 분리할 수 없을 것 같다고요?
하지만 대부분의 퍼즐이 그렇듯
클로버 퍼즐도 마술 같은 해법이 있습니다.
바로 '매듭'의 성질을 이용하는 거죠.
2
수학에서 말하는 매듭
철사를 엇갈려 만든 세잎클로버를
끈이라고 생각하고 양 끝을 당기면
매듭이 만들어지는데,
이 매듭을 연구하는 매듭 이론이 해법의 핵심입니다.
'매듭' 하면 우리는 신발에 묶인 끈처럼
'꼬인 끈'을 떠올리는데요.
매듭 이론에서 말하는 매듭은
조금 다릅니다.
위상수학에서는 머그컵과 도넛처럼
자르거나 구멍을 내지 않고
어떤 물체와 똑같이 만들 수 있으면
두 물체를 같은 것으로 생각하죠?
매듭도 마찬가지입니다.
아무리 단단하게 묶은 끈도
양 끝이 떨어져 있으면 시간이 걸릴 뿐
언젠가 풀 수 있어 묶이지 않았다고 생각하죠.
이런 이유 때문에
끈을 아무리 조작해도 풀 수 없도록
양 끝을 이어붙인 끈이 수학에서 말하는
'진짜' 매듭입니다.
이제 이런 매듭의 특징을 살펴보며
클로버 퍼즐의 해법을 찾아봅시다!
3
세잎매듭을 풀려면 매듭을 만들어라(?)
클로버 퍼즐의 해법이 꽤 어려우니
단계적으로 생각해보겠습니다.
먼저 딱 봐도 나무 공의 지름이
고리의 지름보다 크기 때문에
고리를 나무 공쪽으로 빼는 건 불가능합니다.
따라서 방법은 세잎클로버
장식의 한쪽부터 통과시켜서
반대쪽 끝으로 빼는 겁니다.
문제는 고리의 움직임을 방해하는 끈인데요,
클로버 퍼즐을 풀려면 이 끈을 처리할 방법을 알아내야 합니다.
만약 끈을 적절히 움직여
아래 그림처럼 세잎클로버에 딱붙게
할 수 있다면 고리를 쉽게 분리할 수 있겠죠?
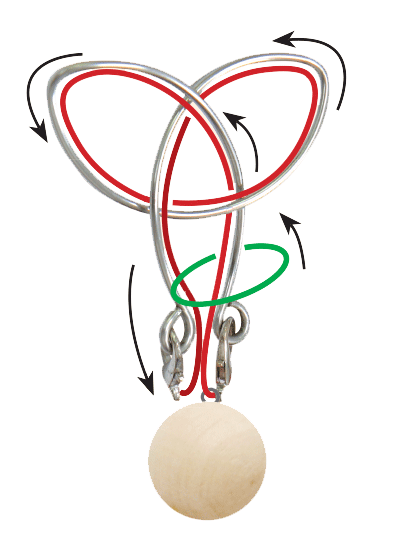
그림①
하지만 문제는 끈을 이렇게 만들 수 없다는 겁니다!
위 그림에서 철사와 끈을 쭉 펴면
‘영매듭’이 되는데
클로버 퍼즐은 ‘세잎매듭’이기 때문에
아무리 변형시켜도 영매듭으로 만들 수 없죠.
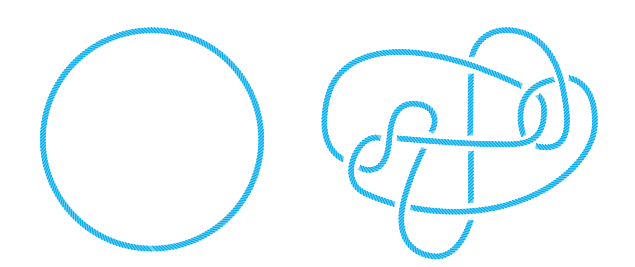

그림②
교차점이 없는 '영매듭(왼쪽, 중간)'과 교차점이 3개인 '세잎매듭(오른쪽)'. 원은 끈 끼리 한 번도 교차하지 않지만, 수학에서 0을 수라고 생각하는 것처럼 원도 매듭이라고 본다. 가운데 매듭처럼 영매듭을 비틀고 꼬아 만든 매듭도 차근차근 풀면 원래대로 되돌릴 수 있어 똑같은 영매듭이다.
영매듭 다음으로 기본이 되는 매듭인 ‘세잎매듭’은 영매듭과 달리 끈이 꼬여 있기 때문에 끈을 아무리 움직여도 영매듭으로 만들 수 없다. 클로버 퍼즐에서 세잎클로버 장식이 달린 목걸이는 한쪽이 축 늘어진 세잎매듭이다.
그런데 이 문제는 쉽게 해결할 수 있습니다.
아래 그림처럼 세잎클로버의 한쪽 끝에
작은 세잎매듭이 만들어지도록 하면
철사와 끈이 기존 매듭을 유지하면서도
고리가 통과할 수 있거든요.

그림③
위 그림처럼 만드는 방법은 여러분에게 맡기겠습니다.
도전해보고 궁금한 것이 있으면 댓글에 남겨주세요!

KPP 한동규 님이 직접 만들어 보여준 클로버 퍼즐의 해법.
--------------------------------
함 께 풀 어 보 세 요
1.
그림②의 가운데 매듭을 왼쪽 매듭으로 바꾸는 방법은 무엇일까요?
직접 매듭을 만들어 시도해보세요.
2.
클로버 퍼즐을 그림③처럼 만들려면 끈을 어떻게 움직여야 할까요?
3.
세잎매듭을 좌우로 대칭해 만든 매듭을 원래 매듭으로 만들 수 있을까요? 불가능하다면, 그 이유는 무엇일까요?
-끝-











