이 정보는 임용수학-위상수학문제집에서 나온 정보들입니다
무한대를 샐수 있다는 말은 우수기사 중에 있습니다
하지만 저는 수학적인 용어로 풀이하려고합니다
데카르트곱 집합  여기서 C를 데카르트곱집합이라고 부릅니다
여기서 C를 데카르트곱집합이라고 부릅니다
여기서  에서
에서  을 이항관계라고 합니다
을 이항관계라고 합니다
간추려서 "관계"라합니다
여기서
 을
을 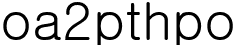 로정의합니다 이것의 역도 성립합니다
로정의합니다 이것의 역도 성립합니다
함수의 정의란
 입니다
입니다
그이유는 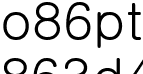 에서
에서 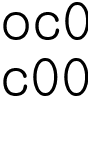 여기서
여기서 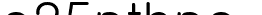 들을 하나의 순서쌍으로 보면
들을 하나의 순서쌍으로 보면
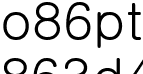 에서 a는 조건이되며, b는 결과가됩니다 즉, a는 정의역, b는 공역이란 것입니다
에서 a는 조건이되며, b는 결과가됩니다 즉, a는 정의역, b는 공역이란 것입니다
집합에서
가산집합, 비가산집합, 유한집합이란 것이 있습니다
유한 집합은 집합 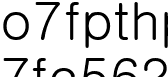 에대하여
에대하여 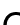 로가는 전사함수가 존재하고
로가는 전사함수가 존재하고
집합 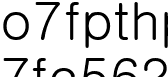 에대하여
에대하여 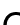 로가는 단사함수가 존재하면
로가는 단사함수가 존재하면
A는 B에대한 유한집합이라고 불립니다
이유: 전단사원리에서 각각의 유일한 값이 존재하므로 정의역, 치.공역이 정해져있다
이걸 바꿔말하면 공역의 수가 정해져있단 뜻으로 유한의 정의에 의하여 유한집합이라고 불린다
가산집합은
위의 조건에서 전사함수를 뺀 집합이다
여기서 가산집합이 유효집합이 아닐때
무한 가산 집합이라고 불린다
비가산집합은
가산집합을 제외한 집합을 말합니다 즉, 가산집합을 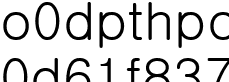 라하면
라하면
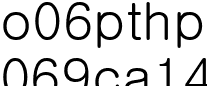 여기서 N은 비가산집합 입니다
여기서 N은 비가산집합 입니다
무한 가산 집합은
단사 원리에서
각각의 값들이 유일하게 할당되어 있으므로 치역은 정해져있다는 뜻이다 공역은 정해지지않았을수도 있어도 치역이 정해져있다
따라서 출력값이 샐수있다라는 것이다
근데 이것은 유한집합을 제외 하였으므로
유한하지 않을 수 있다
따라서 이럴때 "샐수 있는무한"이라고 정의를 내린다
근데 유한집합도 무한할 수 있다
전단사원리를 기본으로 하기때문이다
예를들어 자연수의 집합이있을때
1번째 자연수는 1이고
2번째 자연수는 2이고...
...
...
그러면
f(n) = n으로 정리할 수 있다
함수의 정의의 의해
관계로 분해하면
A는 자연수의 집합
B는 자연수의 집합이다
이는 모두 전단사원리의 만족하므로
유한집합이지만
자연수의 공역은 무한하다
따라서
이는 샐수있는 무한이다
퀴즈: 1. A의 비가산 집합의 여집합은 무한한 유한집합이 될 수 있음을 증명하라
2. 집합 A의 멱집합은 A로서 가는 전사함수가 될수없음을 증명하라 즉, 유한집합이 될수없음을 증명하라