"오늘 3교시는 역사 시험입니다!"
'시험이라고? 공부도 못했는데... 주관식 문제랑 서술형은 포기하고... 객관식 문제라도 풀어야지!'
(시험 끝나기 5분 전)'아악! 10문제는 확실하고, 주관식은 아무렇게나 썼는데, 남은 객관식을 어떻게 하지? 찍을까?'
"땡! 시험 끝! 뒤에서 걷어오세요!"
(허겁지겁 아무거나 찍는다.)
(이미지 출처 : PIXABAY)
혹시 여러분도 이런 경험 있지 않나요? 공부를 열심히 해서 모든 문제를 제대로 풀 수 있으면 좋겠지만, 우리는 가끔씩 모르는 문제의 답을 아무렇게나 고르는, 일명 '찍기'를 합니다.
근데 여러분은 답을 찍을 때 한 번호만 정해놓고 찍나요, 아니면 찍신을 영접받아 생각나는 번호를 찍나요? 이왕 찍는 거, 최대한 많이 맞으려면 어떤 방법이 좋을까요?
<확률을 이용하면 알 수 있지!>
철수는 5지선다형(5개의 보기 중에서 고르는 문제) 시험 문제 20문제를 풀고 있습니다. 그 중 10문제를 이미 풀었고, 10문제는 찍으려고 합니다. 20문제의 답 번호의 개수를 공평하게 분배한다는 가정 하에, 철수는 자신이 푼 10문제의 답을 확인해봤습니다. 그 결과 1, 2, 3, 4, 5번이 각각 2번씩, 즉 모든 번호가 똑같이 나왔다는 것을 알게 되었습니다. 따라서 남은 10개의 문제는 1, 2, 3, 4, 5번이 모두 각각 2번씩 나올 것입니다. 따라서 철수가 1, 2, 3, 4, 5번 중 하나를 골라 계속 같은 번호로 찍는다면 2 문제는 확실히 맞힐 수 있습니다. 반면에 찍신을 내려받아 아무 번호나 막 찍었을 때의 확률은 어떨까요?
하지만 아무 번호나 골라서 찍을 때는 몇 문제를 맞힐까요?
위의 상황에서 한 문제를 맞힐 확률은 
이고, 틀릴 확률은 
입니다. 5개의 보기 중에서 맞는 보기 1개를 선택해 맞거나, 틀린 보기 4개 중 하나를 선택해 틀리기 때문입니다. 그렇다면 두 문제를 연속해서 맞힐 확률은 얼마가 될까요? 어떤 사건 2가지가 동시에 일어날 확률을 구하는 방법을 알면 계산할 수 있습니다. 사건 A가 일어날 확률을 a, 사건 B가 일어날 확률을 b라고 한다면 사건 A, B가 서로 영향을 끼치지 않을 때 두 사건이 동시에 일어날 확률은 a x b가 됩니다.
따라서 두 문제를 연속으로 맞힐 확률은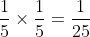 
입니다. 이때, 문제를 n번 연속해서 맞힌다면 그 확률은 
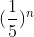이 될 것입니다. 마찬가지로 문제를 n번 연속으로 틀릴 확률은 
5분의 4의 n제곱이 되겠죠? 이 원리를 이용해서 전체 n개의 문제 중에 r개의 문제를 맞힐 확률을 구해봅시다. 전체 문제가 n개이므로 틀린 문제의 개수는 (n-r)개가 됩니다. 따라서 n문제 중 r문제를 맞힐 확률 = 
일 것입니다. 왜냐하면, 전체 문제 중 r문제를 맞히는 일과 n-r개를 틀리는 일이 동시에 일어나는 확률이기 때문입니다. 자, 그러면 10문제 중에서 r문제를 맞힐 확률을 알아볼까요?
| r개 | 0개 | 1개 | 2개 | 3개 | 4개 |
| 확률 | 10.7% | 26.8% | 30.2% | 20.1% | 8.8% |
(모든 확률은 소수점 아래 2번째 자리에서 반올림하여 나타냈습니다.)
휴우... 계산기 돌리랴, 암산하라 힘드네요. 그런데 아직 4문제를 맞힐 확률까지밖에 못 계산했다니!(절망)
하지만, 머리가 나쁘면 몸이 고생하듯 저처럼 힘들게 계산하실 필요가 없습니다. 이것도 '확률'을 이용하면 되니까요.
어떤 사건 A가 일어날 확률 p는 항상 0≤p≤1 입니다. 따라서 무조건 일어나는 일은 확률이 1이겠죠? 중첩되지 않는 사건 A에 대해, A가 일어날 확률은 p이고 일어나지 않을 확률을 q라고 한다면, q = 1 - p입니다. 따라서, 아무렇게나 찍어서 두 문제 이상 맞힐 확률은 1 - (두문제 이상 맞히지 못할 확률)일 것입니다. 따라서, 아무렇게나 찍는다면 100% - (10.7% + 26.8%) = 약 62.5%의 확률로 2문제 이상을 맞히게 됩니다. 같은 방식으로 3문제 이상 맞힐 확률은 42.4%로 생각보다 괜찮은 확률입니다.
잠깐! 그렇다고 항상 아무렇게나 찍어야 맞을까요?
그렇지 않습니다. 실제로는 더 많은 변수가 들어가기 때문입니다.
먼저, 대부분의 시험문제는 보기가 고르게 분배되지 않기 때문에 확률이 크게 바뀔 수 있습니다.
오지선다형 문제가 고르게 1 문제씩 있다고 가정했는데 만약 모든 문제의 답이 5번이었다면 확률과 크게 맞지 않기 때문입니다.
또, 답의 개수에 따라 다를 수 있습니다. 예를 들어 1, 2, 3번 문항이 2번, 4, 5번 문항이 3번 답인 시험의 경우 실제 정답이 (1, 2)이거나 (1, 3)이거나 (1, 4)이거나... 이렇게 너무 많은 경우의 수가 나오기 때문입니다. 이런 경우에는 위에서 만든 공식이 적용되지 않을 수도 있답니다.
마지막으로 시험 문제의 개수나 시험 문제의 종류(O/X문제, 사지선다형, 선긋기 등등...)에 따라 당연히 확률도 달라지겠죠?
따라서 경우에 따라 유리한 찍기 방식이 바뀐다는 것을 알 수 있습니다. 여러분도 앞으로 시험에서 찍을 때는 조금 더 똑똑하게 찍는 건 어떤가요?
아 참, 찍는 것보다는 확실히 공부해서 정정당당하게 문제를 푸는 게 더 좋다는 거! 다들 아시죠?
<오늘의 퀴즈>
철수는 O, X 문제 10문제도 찍으려고 합니다. 선생님이 항상 O와 X를 고르게 분배하신다고 가정한다면 O와 X 중 하나를 골라서 계속 찍는게 나을까요, 아무렇게나 찍는게 나을까요?
(대표 이미지 출처 : PIXABAY)
※ 원래 기사에서 제가 미처 꼼꼼히 보지 못하고 넘어간 오류가 몇 개 있었습니다. 결과에는 변화가 없지만 nCr을 곱해주지 않아서 여러분도 혼동을 겪었고, 각각의 확률이 크게 달라져서 수정했습니다. 정말 죄송합니다. ㅜㅜ
또한 두 번째 경우였던 8문제 중에 찍는 부분은 위에서 말했다시피 지나치게 경우의 수가 많아 계산이 복잡해져서 삭제했습니다. 또한 단위나 몇가지 표현을 수정했습니다. 불편을 드려 정말정말 죄송합니다! ㅜㅜ
#확률 #찍기 #찍신
