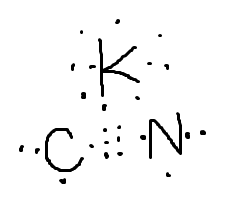

이렇게 안해주셨음 합니다. 저 5학년이거든요^^ 자신한텐 질 낮은 문제가 아닐수도 있잖아요 ,,
-
그래도 저건 너무 쉽지 않나요?
최종 문제를 5단계에 걸쳐서 푼다면 저건 1단계쯤에 해당하는거죠.
예:빨간연필 7개랑 노란연필 4개랑 초록연필 3개가 있다. 빨간연필과 초록연필을 포개면 투명해서 노란연필이 된다.
가능한 경우의수는?에서 처음으로 할 수 있는 행위죠
-
그래도 상위 개념으로 너무 쉽게 풀리는 문제는 아니라고 봅니다.
초1이 낸 문제라도 상위 학생이 보았을 때 바로 풀리지 않을 정도의 문제의 수준은 필요하다고 생각합니다.
예)1 100개가 있다. 여기 사이사이에 원하는 사칙연산을 넣어서 최대로 만들자.(초2부터 만들수있으며 초2~고3이 도전해볼수있죠)
-
...전 질이 아니라 성의로 판단해야 한다고 생각합니다
좋아요0 -
그런데 처음엔 저도 그렇게 생각했는데... 사실 그렇게 덧셈만으로 어려운 문제를 만드는 게 말이 쉽지 실제로 해 보면 그렇게 할 수 있는 학생들은 수학을 비교적 잘 하는 학생들 안에서도 초천재가 아닌 이상 아마 1%도 안 될 것 같습니다. 그런 식으로 하려면 완전히 그것을 100%이해하는 것으로도 모자라서 한층 더 깊게 들어가서 자유자재로 다룰 수 있는 능력이 필요하거든요. 저 같은 경우, 초 2때 365÷14라는 나눗셈을 푸는 방법을 책에서 읽었는데, 그 방법을 정말 오래 걸려서 알게 되었어요. 만약에 그때 폴리매스가 있었고 제가 폴리매스에 726÷32의 몫과 나머지를 계산하라는 문제를 냈다고 생각해보세요. 그때의 저라면 365÷14도 완전 어려웠는데, 그것을 한층 변형시켜 726÷32로 내는 것은 나눗셈에 대해 100%완벽히 이해해야 가능한 일이죠. 따라서 그때의 저라면 저 정도 수준도 정말 질 좋고, 성의도 매우 많이 들어간 문제였을 겁니다. 그런데 폴리매스는 주로 초 5 이상인 분들이 많죠. 그 분들이 본다면 저 문제는 당연히? 질이 낮다고 하겠죠. 그러면서 '다음부턴 이런 문제 삼가해달라'라고 하면 정작 본인은 엄청 열심히 냈고, 더 이상 이 수준에서 더 어려운 문제를 내는 건 거의 불가능에 가까운데 '아니 열심히 만들었는데 질이 나쁘다고 하는 사람들은 뭐지? 내 수준에서 어떻게 이것보다 잘 만들어?'라고 생각하겠죠(tmi지만 더군다나 그때 당시 저는 다른 사람들에게 문제 내는 걸 매우 좋아하던 스타일이었습니다). 나눗셈을 처음 배운 수준에서 그런 문제를 내는 건 거의 천재에 가까운데 말이죠. 암튼 본론으로 돌아가면, 그렇게 하는 게 중 2 기준에서 보니 말이 쉽지 초 2 기준에서 보면 나눗셈도 아주 많은 성의가 들어가야 만들 수가 있다는 겁니다. 솔직히 초 2 정도면 천재가 아닌 이상 아직 배운 것이 거의 없는데 거기서 중 2 기준으로 좋은 문제를 내달라는 건 '무에서 유를 창조하라'라고 하는 것과 똑같습니다. 그래서 저는 개인의 능력에 맞춰서 질 좋은 문제, 질 나쁜 문제의 기준이 많이 달라질 수 있다고 생각합니다. 그러나 문제를 낸 성의는 객관적이지 않나요? 누가 보기엔 쉬울 진 몰라도, 성의는 '이 사람이 그 정도 수준이면 정말 열심히 만든 문제구나'라고 생각하죠. 따라서 저는 질보다는 성의를 기준으로 나눠야 한다고 생각합니다.
좋아요0 -
그리고 저희가 내는 문제도 대학생이나 세계적인 수학자 기준에서 본다면 이 상황과 다를 게 없다고 봅니다. 만약 휠릭님이 미적분을 겨우겨우 이해하고 본인이 직접 미적분 문제를 만들어 냈는데, 수학자들이 '너무 쉬운 것 아니냐. 이런 문제는 안 냈으면 좋겠다'라고 한다면요? 이 상황과 뭐가 다르죠?
좋아요0 -
어과동 시끌벅적 토론터같다(ㄷㄷ)
거긴 대체로 나이가 어린 사람이 많아서 한 줄 띡 쓰고서는 반박 들어와도 무시하는 사람많던데요
제가 대략 토론을 3번 했었는데 1번은 다른 사람 의견에 반박을 했어요.
그래서 다음날 재반박이 달렸는데;;; 제가 그걸 다시 재반박했습니다
그런데 그 이후 15일째 저는 아무 댓글도 받지 못했습니다(
갑자기 제 얘기는 왜 나온거죠)좋아요0 -
나누기에서 숫자만 바꾸는 것은 365/14를 계산하는 방법을 안다면 같은 방식으로 계산 기계가 되었다고 생각하면 못하면 시간은 걸리더라도 726/32도 같은 문제라고 봐야 합니다.
마찬가지로 제가 미적분을 겨우 이해하고 와서 문제를 냈습니다. 아마 기본적인것만 넣어서 냈겠죠. 그럼 당연히 다른사람들은 하지 말아달라고 할겁니다. 그럼 전 '이건 너무 쉬운거였나'하고 거기에 대해서 더 찾아볼 수 있는 계기가 될 수 있겠죠 제가 미적분은 모르기떄문에 얼마나어려운지도 모르지만
아무리 초2가 문제를 낸다고 하더라도, 초 4개념으로 푸는 문제라면, 초4기준에서 질이 낮은지 확인해야 한다고 생각합니다. 나눗셈은 초3~4에 배우죠. 우리의 머리가 그때 그걸 받아들일 정도로 발전하였기 떄문입니다. 그러니 무리하게 윗 학년꺼를 아주 쉽게 내는 것 보다는, 자신의 수준 안에서 어려운 문제를 내는 것이 낫다고 생각합니다.
덧셈만 배운 1학년 같은 경우에는 덧셈만 이용한 유익한 문제를 내볼 수 있겠죠. 굳이 힘들게 이해한 뺄셈을 가지고 와서 5+8-9를 계산해봐 이렇게 할 이유는 없습니다.
좋아요0 -
네, 뭐 그렇게 생각하실 수도 있겠죠. 휠릭님과 엔뚀님이 처한 상황 자체가 다르니까요. 방금 댓글에서 '그런 상황에 처한다면 미적분을 더 찾아보고 내겠다'라고 하셨죠. 그러나 제 경험상 (물론 수학의 모든 분야가 다 그렇지만) 미적분은 인강, 백과사전, 책 같은 걸로 딱 본다고 자유자재로 다룰 수 있는 게 아닙니다. 처음에 딱 보면 '아, 그렇구나'하면서도, 나중에 다시 떠올리면 어디서부터 손을 대야 할지 막막해집니다. 이처럼 미적분도 그렇고 기하, 조합 같은 것도 그렇고 심지어 덧셈도 처음 배울 때는 그렇게 어려운 문제를 만들기란 거의 불가능에 가깝습니다. 그렇게 하려면 그 개념을 완전히 이해하고도 모자라 자유자재로 다룰 수 있어야 하는데, 그게 어디 한 번 보고 딱 되는 일은 아니잖아요? 그렇게 하려면 아주 오랜 시간이 소요되어야 하죠. 다시 말하면, 그런 식으로 어려운 문제를 자유자재로 만들려면 진짜 최소로 잡았을 때 한 달은 넘게 필요하다는 겁니다. 이러면 휠릭님이 어떤 반론을 내세울지 예상이 갑니다. 아마 '그러면 이해가 될 때까지 반복 학습을 하면 되지 않냐'고 하겠죠. 그러나 수동에도 나왔지만, 직접 문제 내보기가 수학 공부를 할 때 아주 효과적입니다. 그런 문제를 내면서 최선을 다해서 내기만 했으면 거기에 대해 모호했던 개념들이 딱 잡히잖아요? 수학을 배울 때 '직접 출제자가 되어 보기'가 매우 효과적이죠. 문제를 내고 다른 사람이 푼 걸 보면서 모호했던 개념이 딱 잡히니까요. 물론 이럴 경우는 문제를 '최선을 다해 냈을 경우'만 해당이 됩니다. 그러나 제가 봤을 때, 그 문제는 대충 낸 문제는 아닌 것 같다고 판단이 됩니다. 더군다나 엔뚀님은 자신이 배우고 있는 진도를 예전에 공개한 적이 있어요. 그 정도 수준이면 저런 문제도 절대 대충 낸 문제라고 판단이 되지 않습니다. 뭐 지금은 미적분을 배우지 않았으니 앞의 내용이 잘 공감이 안 될 수도 있습니다. 그러면 나중에 미적분을 배우고 문제를 한 번 내 보세요. 아마 이미 미적분을 배운 분들이라면 질이 낮다고 하겠죠. 그런데 과연 그 문제가 쉽게 만들어질까요? 미적분을 '자유자재로' 다뤄야 가능한 일인데요? 그런 식으로 처음에 배웠을 때 '우리 기준에서 질 좋은 문제를 내달라'고 하는 건 '처음에 배웠을 때 자유자재로 사고해달라'라고 하는 거랑 똑같고, 이는 '무에서 유를 창조하라'고 하는 것과 똑같습니다. 정작 본인은 열심히 만들었는데 말이죠. 문제의 질은 사람에 따라 얼마든지 달라질 수 있다고 생각합니다.
좋아요0 -
와...타인님
긴글을 읽기 쉽게 쓰다니 대단하십니다.
단순문제를 금지하는건 홈페이지 관리하는 측에서만 가능하다고 생각되고,
그냥 자기 나름대로 단순문제는 지적해줄수있다고 생각합니다.
그냥 이용자들은 자신의 의견을 말할 뿐이죠.
좋아요0 -
타인님 마ㄹ에 공감합니다
좋아요0
-
-
그런데 다들 뭐라고 하면서 푸시는 건 뭔지... 저는 뭐라고도 안하고 안 풀겠습니다. 어쩌피 다른 사람들이 한 번 지적한 것 같으면 또 굳이 지적을 할 필요는 없지만 그래도 앞으로는 좀 더 문제에 살을 붙여서 만들어주시면 감사하겠습니다.
-
엔뚀 님 힘내세요!
문제가 좀 쉽다는 의견이 있더라도
전 엔뚀님께서 열심히 내셨을 거라고 믿습니다.
그래도 휠릭님의 의견도 아주 틀린 것 같지는 않으니....
이건 어떤가요? 문제에 좀 더 스토리를 넣어서, 기본적인 개념으로 푸는 문제라도 어려워보이게 만들거나 재밌게 만드는 거죠! ㅎㅎ
이상 폴리매스 랭킹 20 내 가장 멍청한 사람의 의견이었습니다.
-
우리 반모..
좋아요0 -
그러게요...
저도 처음 문제 보고서 솔직히;; 소올직히는 뭐라뭐라 태클 걸려고 했습니다.
그런데 뭐 엔뚀언니는
선행진도가 저보다 느리니까그럴 수도 있다고 생각해요.게시판에 질 낮은 문제 내지 말라고 글도 올라왔는데 (게다가 그 글들은 다 맨 위에 고정되어 있죠)
엔뚀언니가 그걸 다 무시하고 쉬운 문제를 냈을 리는 없지 않겠어요?
그렇지만 휠릭님도 틀린 의견은 아닙니다. kmo공부하는 사람 입장으로써는 사실 암산 0.1초컷이긴 합니다.
게시판에 나이도 공개하고 진도도 공개했는데 그런 문제 냈다고 뭐라 하는건 저도 좀 그렇다고 생각합니다.
그니까 결론적으로는 음... 저처럼 아주아주 쉬운거에 겁나 복잡해 보이게 10줄이고 20줄이고 간에 스토리든 예시든 가져다 덧붙이는겁니다.
그러면 kmo나 더 높은거 공부하시는 분들도 출제하는데 고생하셨겠구나 하고 저렇게 욕하지는 않을거에요 ㅎㅎ
(예시로 그 문제를 들어보죠)
버블몬의 학교에서는 3문제의 OX퀴즈대회를 열기로 했다.
버블몬은 상품을 받고 싶어 참가를 하였지만 답을 모른다. 그래서 버블몬은 모든 문제를 무작위로 제출하려고 한다.
버블몬이 OX퀴즈를 모두 맞출 확률은?
---------
근데 이렇게 붙여도 제가 읽어보니 이건 쉽긴쉽네요;;;;
그렇지만 저보다 문장력 좋으실테니 요런 방법 추천해드립니다.
 좋아요0
좋아요0 -
버블몬님 공감합니다. 사람들마다 수준이 다를 수도 있잖아요? 그리고 여기선 저보다 나이 많은 사람들이 거의 다일 것이고, 아마 저보다 훨씬 많이 나가..
좋아요0
-
-