국가수리과학연구소 21번
내맘대로 숫자 레시피
문제 출제자 : 백진언 수리과학연구소 연구원
문제1
아래 숫자 5개를 전부 한 번씩만 쓰고, 사칙연산과 괄호만 이용해 숫자 38을 만들어라.
1 4 5 5 5
문제2
1 이상, 9 이하의 숫자 5개를 고른 뒤, 이 숫자 5개로 문제1과 같은 방법으로 1부터 연속한 자연수를 가장 많이 만들 수 있는 방법은 무엇일까? 이때, 자연수는 1부터 연속해서 어디까지 만들 수 있을까? 예를 들어, 1 다섯 개로는 1부터 6까지의 수는 만들 수 있지만, 7과 8은 만들 수 없다.
※오타를 수정합니다.
문제2 4번째 줄에 '1부터 7까지의 수'가 아니라, '1부터 6까지의 수'입니다.
※알립니다.
①누군가 친구가 소문제 1번을 해결했어요. 다들 정답을 확인해 보세요!!
②소문제 2번은 수돌이 친구가 최초로 풀고, 이어 수학자 & 누군가 친구가 잇달아 풀었습니다. 문제 특성상 3명이 공동으로 푼 걸로 인정하겠습니다. 프로그래밍으로 문제를 해결할 때 어떻게 풀이를 검증하는지 잘 알아두세요!!
-
문제 1 증명과정
/
mod 5로 보자.
38은 mod 5로 3이다.
1,4,5,5,5로 3 (mod 5)를 만들 수 있는 것은 (4-1)밖에 없다.
즉 3,5,5,5로 38을 만드는 것과 동일한데,
이는 불가능하다.
/
혹시 이 증명에 오류가 있나요?
-
39,37,36,35,34같은건 만들겠는데 38은 아직 못만들었네요ㅠ
41- (5+5)/5 = 39
51-(4+5+5) = 37
55-4×5+1 = 36
155÷5+4 = 35
54-(5+15) = 34
-
출제자 님께 등판을 요청했지만, 바쁘신 관계로 의견만 전달!
①숫자 1, 2를 12로 붙여쓰는 건 불가!
②문제 마지막에 "8은 만들 수 없다"는 오타가 아님!
(단, 연속된 숫자를 못만든다는 의미를 강조하기 위해 8 앞에 7을 추가하겠습니다.
 )
) -
-
1=3÷(1+2)×(5-4)
2=(4-(5-3))÷2+1
3=5×2-4-3×1
4=4×(5-3-2+1)
5=5×((3+2)×1-4))
6=(5+1)×(2+3-4)
7=(5+2)×(4-3×1)
8=(5+3)×(4-2-1)
9=(5+4)×(3-2×1)
10=(5+4+1)×(3-2)
11=(5+4+3-2+1)
12=(5+4+3)×(2-1)
13=(5+4+3+2-1)
14=(5×3)-(3-2×1)
15=(5+4+3+2+1)
16=(5×4-3-(2-1))
17=(5×4-3×(2-1))
18=(5×4-3+2-1)
19=(5×4-(3-2×1))
20=(5×4×(3-2×1))
21=(5×4+(3-2×1))
22=(5×4+(3+1-2))
23=(5×4+3×(2-1))
24=(5×4+3+2-1)
25=(5×(4+1)×(3-2))
26=(5×(4+1)+(3-2))
27=(5×(4+2)-3×1)
28=(5×(4+2)-(3-1))
29=(5×(3+2)+4×1)
30=(5×(4+1)+3+2)
31=???
좋아요0 -
동참해 주실분 구합니다.
그런데 예상보다 많이 나오네요...
프로그래밍 등 다른 방법이 필요할 것 같습니다.
좋아요0 -
14에 3이 2개 있으셔서 14 = 3 x 4 + (5-2-1)
로 다르게 나타내봤어요.
그리고 31부터는..
31 = (5+2) x 4 + 3 x 1
32 = (5+2) x 4 + 3 + 1
33 = (5+3) x 4 + 2 - 1
34 = (5+3) x 4 + 2 x 1
35 = (5+3) x 4 + 2 + 1
36 = ( 5 + 3 + 2 - 1 ) x 4
37 = 2 x 4 x 5 - 3 x 1
38 = (5 + 3) x (4 + 1) - 2
39 = (1+5) x (4+2) + 3
40 = (4+2-1) x (5 +3)
41 = (2x5+4) x 3 - 1
42 = 5 x (4+3+1) + 2
43 = (2x5 +4) x 3 + 1
44 = (5 x 4 +2) x(3 - 1)
45 = (3x1 +2) x (5+4)
46 = 2 x (4 x 5 + 3 x 1)
47 = 2 x (4 x 5 + 3) + 1
48 = 4 x (5 x 2 + 3 - 1)
49 = (3 + 4) x (2 + 5) x 1
50 = 5 x (1+2+3+4)
51 = 3 x (4 x 5 - 1 - 2)
52 = 4 x (1 x 2 x 5 + 3)
53 = 5 x (3 x 4 - 1) - 2
54 = (5 + 4x1) x 3 x 2
55 = 5 x (3 x 2 + 4 + 1)
56 = (3 + 4) x (1 + 2 + 5)
57 = 3 x 4 x 5 - 2 - 1
58= 3 x 4 x 5 - 2 x 1
59 = 3 x 4 x 5 - 2 + 1
60 = (1 + 4 + 5) x 3 x 2
61 = 3 x 4 x 5 + 2 - 1
62 = 3 x 4 x 5 + 2 x 1
63 = 3 x 4 x 5 + 2 + 1
64 = (3 + 5) x (1 x 2 x 4)
65 = (3 + 5) x 2 x 4 + 1
66 = (1 + 5) x (4x2 +3)
67 = ??
일일이 나열하면서 문제에 도움이 될 성질이 무엇일지 찾아야겠단 생각이 들어요..
1번문제는 불가능할 것 같단 느낌만 드는데.. 불가능한 이유를 찾아보려해요.
좋아요0 -
혹시 1,2,3,4,5 로 74나 76을 만들 수 있나요?
1~73, 75, 77은 만들 수 있어요.
좋아요1 -
74 = (5+1) x 4 x 3 + 2를 찾았어요.
좋아요0 -
권순용님이 물어보셨던 건 아니지만 78 = (3 + 1) x 5 x 4 - 2도 찾았어요.
좋아요0 -
요 대댓글과 별개지만 1,2,3,4,5말고 3,4,5,7,9를 쓴다면 76도 가능합니다.
76=3 x 4 x 5 + 7 + 9
좋아요0
-
-
문제2번 1~9중 5개 고를 때 1,2,3,4,5같이 서로다른 경우 말고도
1 4 5 5 5처럼 서로 같은 수를 여러 번 골라도 괜찮은건가요?
-
1,2,3,4,5뿐만 아니라 2,5,3,8,6등 5!=120가지(중복이 가능하다면 55=3125가지)나 살펴봐야 합니다. 제 생각에 손으로 계산하는 건 영 아니라고 보는데요.
-
계산해 보니 수의 배치 방법 20가지, 연산기호 배치 4^4=256가지, 괄호의 배치 방법 42가지로 총 약 21만 가지입니다.
코딩으로 해결하기 충분한 문제네요.
-
그것을 찾아봐서 없으면 답 확정이네요
좋아요0 -
/resources/comment/2018/09/2c77b3ae040cdda527bbde3938d81180.cpp
(1)번 문제 코딩으로 풀었습니다. 답 없습니다.
코드가 상당히 긴데, 파일로 첨부합니다.
좋아요0 -
코드에 사소한 오류가 있었네요. 수정했습니다. 역시 답 없습니다.
/resources/comment/2018/09/874d1003d0eec65663ef7b301ac1badf.cpp
좋아요0 -
백진언 연구원님에 따르면, 코드에 오류가 있는 것 같다고 합니다! 과연 정답이 있는 걸까요, 없는 걸까요??
 좋아요0
좋아요0
-
-
처음 수를 x1 , y1 으로 시작하고 이 두가지로 할 수 있는 연산이 6가지니깐 처음 연산한 결과를 x2 다른 숫자를 y2 로 했을 때 이를 x4 , y4 까지 가게 해야하니 64 가지가 되고 이는 1296이니 1296가지 이네요. (문제 1)
-
-
나올 수 있는 괄호의 경우를 저는 42가지로 분류했거든요. (N은 수, O는 연산자)
가짓수가 더 있을까요?
"NONONONON", "(NON)ONONON", "(NONON)ONON", "(NONONON)ON", "NO(NON)ONON",
"NO(NONON)ON", "NO(NONONON)", "NONO(NON)ON", "NONO(NONON)", "NONONON(ON)",
"((NONON)ON)ON", "((NON)ONON)ON", "(NO(NONON))ON", "(NO(NON)ON)ON",
"(NONO(NON))ON", "((NON)ON)ONON", "(NO(NON))ONON", "(NONON)O(NON)",
"(NON)O(NONON)", "(NON)O(NON)ON", "(NON)ONO(NON)",
"NO((NONON)ON)", "NO((NON)ONON)", "NO(NO(NONON))", "NO(NO(NON)ON)", "NO(NONO(NON))",
"NO((NON)ON)ON", "NO(NO(NON))ON", "NO(NON)O(NON)", "NONO((NON)ON)",
"(((NON)ON)ON)ON", "((NO(NON))ON)ON", "((NON)O(NON))ON",
"((NON)ON)O(NON)", "(NO((NON)ON))ON", "(NO(NO(NON)))ON", "(NO(NON))O(NON)",
"(NON)O((NON)ON)", "NO(((NON)ON)ON)", "NO((NO(NON))ON)", "NO((NON)O(NON))",
"NO(NO((NON)ON))"
-
/
mod 5로 보자.
38은 mod 5로 3이다.
5를 곱하면 mod5로 0이 된다.
또한 5를 더하는 것 또한 mod5로 변화를 주지 않는다.
따라서 1,4만으로 3을 만들어야한다.
이때 1,4,5,5,5로 3 (mod 5)를 만들 수 있는 것을 두 종류로 나누어 확인해보자
1) 3을 만들때 5를 사용하지 않을 경우
(4-1)이 유일하다.
3,5,5,5로 38을 만들 수 없다.
2) 3을 만들때 5를 사용할 경우
1,4를 (5-4)혹은 (5-1)로 사용하거나
5에 1,4를 더한 후 곱해야 의미가 있다.
2-a-1) (5-4)사용
1,1,5,5 사용하는 것과 동일.
38은 만들 수 없다.
2-a-2) (5-1)사용
4,4,5,5 사용하는 것과 동일
38은 만들 수 없다.
2-a-3) (5-1), (5-4) 사용
1)과 동일
2-b-1) (5-4)와 곱할 때
1,5,5 사용하는 것과 동일
38은 만들 수 없다.
2-b-2) (5+4)와 곱할때
1,9,5,5 사용하는 것과 동일 (9는 곱하는 용도)
38은 만들 수 없다.
따라서 불가능하다.
/
처음 이용한 방식을 응용해 보았습니다.
나중에 시간날때 완성시키겠습니다.
오류 지적해 주시면 감사하겠습니다.
-
-
문제1번 답
(4-(1/5))*(5+5)
스크래치로 모든 경우의수를 확인하여 찾았습니다.
https://scratch.mit.edu/projects/246053946/
-
누군가 친구 정다아아아아아아압!
 부분해결 딱지 부착입니다!좋아요0
부분해결 딱지 부착입니다!좋아요0 -
와우! 이런 방법이 있었군요!
답이 없을것 같았는데, 이런 답이 있었네요.
놀랍습니다!
좋아요0 -
몇 줄만 고치니 이 네 가지 나오네요.
(4-1/5)*(5+5): 38.00000
(5+5)*(4-1/5): 38.00000
(4-(1/5))*(5+5): 38.00000
(5+5)*(4-(1/5)): 38.00000보니까 아예 소수 계산이 안 되고 있었네요. 아쉬워라... (그리고 괄호 쌍 한 가지 더 있었네요.)
좋아요0 -
비밀 댓글이 등록 되었습니다!
-
비밀 댓글이 등록 되었습니다!
-
-
2번의 모든 경우를 계산 해볼 수 있는 코드는 있으나 최적화는 전혀 되어있지 않아 다 계산 하려면 100시간 정도( 소요될 것 같습니다...........(숫자 배열 하나당 6초,중복배열수9^5,(6×9^5)/3600=~=100)
https://scratch.mit.edu/projects/246059976/
-
2번문제 c프로그래밍을 이용한 풀이
먼저 고려해야 할 점: 숫자 다섯 개의 조합 (a,b,c,d,e)는 일반성을 잃지 않고 a<=b<=c<=d<=e로 가정해도 된다. (<=는 같거나 크다를 의미한다)
그리고 (a,b,c,d,e)로 만들 수 있는 수를 찾을 때 (a,b,c,d,e)의 순열에 대해서 고려하므로 (즉, (1,1,1,1,2)의 순열은 2가지, (1,3,4,5,7)의 순열은 120가지..)
a,b,c,d,e가 각각 1이상 9이하인 9^5=59,049가지의 경우는 정확히 한 번 이 시행에 등장한다.
1) 따라서 순서가 정렬되어 있는 (a,b,c,d,e)의 순열의 개수의 총합은 59,049가지이다.
2) 그리고 수와 수 사이 4^4=256가지의 연산기호를 넣을 수 있고,
3) 괄호를 이용한 연산순서의 조정은 다음과 같이 생각해도 된다. 한 번의 연산은 인접한 두 수를 묶어서 하나로 만드는 것이다. 즉 2+3*7+4-3에서 7+4에 연산을 실행하면 2+3*11-3이 되는 것이다. 네 번의 연산을 통하여 다섯 개의 수를 하나로 만들 수 있다. (그래서 연산기호가 총 4개) 4개의 연산자를 어떤 순서로 실행할 것인지 결정하는 것은 4!=24가지가 존재한다. 그리고 그것은 괄호를 통하여 무조건 구현 가능하다. 예를 들어서, 1+2-3*4/5에서 -,*,+,/순서로 연산을 진행한다면 그 순서대로 괄호를 묶어 ((1+((2-3)*4))/5)라는 식이 되는 것이다.
따라서 총 가지수는 362,797,056가지이고, 각 가지수마다 아래의 코드에 의하면 프로그램 내 16~24회의 연산이 필요하다. 따라서 총 연산횟수는 약 72억이므로 예상 소요 시간은 약 72초라고 할 수 있다.
#include <stdio.h>
#include <algorithm>
using namespace std;//프로그램의 시작. next_permutation이라는 특별한 함수를 사용하기 위해서 #include <algorithm>을 선언해준다.
struct fraction{
int u;
int d;
};//소수를 표현하는 float를 이용할 경우 두 변수가 같은지 판별하는데 있어서 오류 위험이 있으므로(반올림) 분수를 구현하는 구조체를 쓰도록 한다. 구조체란, 프로그램 작성자가 원하는 형태의 변수를 만들어 사용할 수 있는 것으로, 여기서는 분모를 표현하는 정수 u, 분자를 표현하는 정수 d를 묶어서 하나의 변수로 사용한다.
struct fraction cal_table[5];
int oper_table[4];
int oper_order[4];
bool checklist[100000];//프로그램에서 사용할 전역변수이다. cal_table은 계산이 이루어지는 배열이고, 처음에는 골라진 5개의 수가 들어갈 것이다.(분모가 1인, 즉 자연수의 형태로) oper_table은 5개의 수 사이사이에 들어갈 사칙연산을 저장하는 배열이다. 0은 +, 1은 -, 2는 *, 3은 /를 의미한다. oper_order은 4번의 연산에서 연산순서를 저장하는 배열이다. 24가지 경우가 존재한다. checklist는 5개의 수를 고르는 각 경우에 대해서 만들 수 있는 수(1)와 만들수 없는 수(0)을 기록한다. 처음에는 0으로 초기화된다.
struct fraction add(fraction a,fraction b){
fraction x;
x.d=a.d*b.d;
x.u=a.u*b.d+a.d*b.u;
return x;
}
struct fraction sub(fraction a,fraction b){
fraction x;
x.d=a.d*b.d;
x.u=a.u*b.d-a.d*b.u;
return x;
}
struct fraction mul(fraction a,fraction b){
fraction x;
x.d=a.d*b.d;
x.u=a.u*b.u;
return x;
}
struct fraction div(fraction a,fraction b){
fraction x;
x.d=a.d*b.u;
x.u=a.u*b.d;
if(b.d==0) x.d=0;
return x;
}//분수들 사이의 사칙연산을 진행하는 함수이다. 나눗셈 연산의 if(b.d==0) x.d=0;를 눈여겨 봐야 하는데, 이 조건이 추가됨으로써 만약 두 분수중 하나의 분모가 0이라면, 연산 결과의 분모도 항상 0이 되어, 최종 결과에서 분모가 0인지 체크하여 불가능한 연산을 판별할 수 있다. (도중에 0으로 나누었는지)
int gcd(int a,int b){
if(a*b==0) return a+b;
if(a>b) return gcd(a%b,b);
else return gcd(a,b%a);
}//두 자연수 사이의 최대공약수를 구하는 함수이다. 유클리드 호제법을 이용하였다.
struct fraction rev(fraction a){
fraction x;
int G;
x.u=a.u>0? a.u:-a.u;
x.d=a.d>0? a.d:-a.d;
if(x.d*x.u!=0){
G=gcd(x.u,x.d);
x.u/=G;
x.d/=G;
}
if(a.u*a.d<0) x.u=0-x.u;
return x;
}//어떤 분수를 약분해주는 함수이다. if(a.u*a.d<0) x.u=0-x.u;를 이용하여 음수이면 분자를 음수로 표기하여 그 사실을 알 수 있게 하였다.
void calculate(int pos){
int i;
if(oper_table[pos]==0) cal_table[pos]=(add(cal_table[pos],cal_table[pos+1]));
if(oper_table[pos]==1) cal_table[pos]=(sub(cal_table[pos],cal_table[pos+1]));
if(oper_table[pos]==2) cal_table[pos]=(mul(cal_table[pos],cal_table[pos+1]));
if(oper_table[pos]==3) cal_table[pos]=(div(cal_table[pos],cal_table[pos+1]));
for(i=pos+1; i<4; i++) cal_table[i]=cal_table[i+1];
for(i=pos; i<3; i++) oper_table[i]=oper_table[i+1];
}//이번에 연산할 연산자의 순서를 입력하면 cal_table 안에서 해당하는 연산자를 실행하여 연산자 양 옆의 두 수를 하나로 묶어준다. 실행한 연산자는 사라진다.
int main(){
int number[5],oper[4],i,isBreak,MAX_value=-1,MAX_num[5],announce=0;//메인함수가 시작된다. 반복문을 돌리기 위한 number[5],oper[4],i, 반복문을 빠져나오기 위한 isBreak, 최댓값을 저장하기 위한 MAX_value=-1,MAX_num[5], 긴 프로그램 런닝타임 동안 현재 진행도를 알려줄 announce=0을 선언한다.
for(number[0]=1; number[0]<=9; number[0]++)
for(number[1]=1; number[1]<=9; number[1]++)
for(number[2]=1; number[2]<=9; number[2]++)
for(number[3]=1; number[3]<=9; number[3]++)
for(number[4]=1; number[4]<=9; number[4]++)
if(number[0]<=number[1] && number[1]<=number[2] && number[2]<=number[3] && number[3]<=number[4])
{//9개 중 다섯 개의 수를 고르는 모든 경우에 대해서 a<=b<=c<=d<=e인 경우만 고려한다.
for(i=0; i<100000; i++) checklist[i]=0;
while(1){
for(oper[0]=0; oper[0]<4; oper[0]++)
for(oper[1]=0; oper[1]<4; oper[1]++)
for(oper[2]=0; oper[2]<4; oper[2]++)
for(oper[3]=0; oper[3]<4; oper[3]++)
for(oper_order[0]=0; oper_order[0]<4; oper_order[0]++)
for(oper_order[1]=0; oper_order[1]<3; oper_order[1]++)
for(oper_order[2]=0; oper_order[2]<2; oper_order[2]++)
for(oper_order[3]=0; oper_order[3]<1; oper_order[3]++)//연산자와 연산순서로 가능한 모든 경우에 대해서 반복한다.
{
for(i=0; i<5; i++) {
cal_table[i].u=number[i];
cal_table[i].d=1;
}
for(i=0; i<4; i++) {
oper_table[i]=oper[i];
}//cal_table과 oper_table에 현재 경우를 복사한다.
for(i=0; i<4; i++) calculate(oper_order[i]);
cal_table[0]=rev(cal_table[0]);//연산을 실행하여 cal_table[0]에 그 결과를 약분된 형태로 저장한다.
if(cal_table[0].d==1 && cal_table[0].u>0) checklist[cal_table[0].u]=1;//분모가 1이고(정수이고) 분자가 양수이면 해당하는 자연수는 만들 수 있으므로 checklist를 1로 만든다.
}
announce++;
if(announce%100==0) printf("%d/59049 has finished\n",announce);//진행도를 표시하는 코드이다.
isBreak=next_permutation(number,number+5);
if(isBreak==0) break;//고른 다섯 가지 수를 나열하는 순열의 경우는 next_permutation이라는 특별한 함수를 사용한다. 이 함수를 호출하면 주어진 배열에서 사전순으로 바로 다음에 있는 순열로 전환해준다. 즉 1,2,3,4,5에서 이 함수를 사용하면 1,2,3,5,4가 되고, 한번 더 호출하면 1,2,4,3,5가 된다. 그리고, 이 함수는 1 또는 0을 반환하는데, 대부분의 경우는 1을 반환하지만, 5,4,3,2,1에서 1,2,3,4,5로 (처음으로) 돌아갈 때만 0을 반환한다. 이를 이용하여 반복문을 탈출할 수 있다.
}
for(i=0; i<100000; i++) if(checklist[i+1]==0) break;
if(i>MAX_value){
MAX_value=i;
MAX_num[0]=number[0];
MAX_num[1]=number[1];
MAX_num[2]=number[2];
MAX_num[3]=number[3];
MAX_num[4]=number[4];
}//만들수 있는 1부터 연속한 수의 최댓값을 계산하고 갱신한다.
}
printf("The Best Case: %d,%d,%d,%d,%d\n Can make number 1~%d",MAX_num[0],MAX_num[1],MAX_num[2],MAX_num[3],MAX_num[4],MAX_value);//가능한 최선의 경우를 출력한다.
}이 코드를 실행한 결과는 다음과 같다.
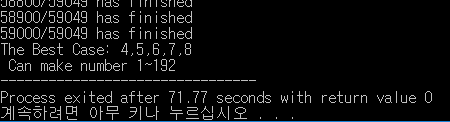
소요시간 71.77초
4,5,6,7,8을 골랐을 때 1~192의 모든 수를 만들 수 있다!
그렇다면 어떻게 만들 수 있을까?
위 코드를 수정하자. 전역변수 checklist를 int checklist[194][14]={0,};와 같이 수정한다. 이제 이 체크리스트는 1~193의 각 경우에 대해 만드는 방법을 저장할 것이다. (193에는 저장되지 않을 것이다.)
메인함수는 다음과 같이 수정한다.
int main(){
int number[5]={4,5,6,7,8},oper[4],i,j,k,isBreak,canvas[60],group[5][2],order;//고른 숫자 4,5,6,7,8을 number배열에 처음부터 넣어준다. 반복문을 위한 변수 j,k를 추가해주고, oper[]와 oper_order[]의 정보를 수식으로 변환하기 위한 캔버스(그림판) 배열 canvas[60], 괄호로 묶을 위치를 저장하는 group[5][2], 현재 연산순서를 저장하는 order를 선언한다.
while(1){
for(oper[0]=0; oper[0]<4; oper[0]++)
for(oper[1]=0; oper[1]<4; oper[1]++)
for(oper[2]=0; oper[2]<4; oper[2]++)
for(oper[3]=0; oper[3]<4; oper[3]++)
for(oper_order[0]=0; oper_order[0]<4; oper_order[0]++)
for(oper_order[1]=0; oper_order[1]<3; oper_order[1]++)
for(oper_order[2]=0; oper_order[2]<2; oper_order[2]++)
for(oper_order[3]=0; oper_order[3]<1; oper_order[3]++)
{
for(i=0; i<5; i++) {
cal_table[i].u=number[i];
cal_table[i].d=1;
}
for(i=0; i<4; i++) {
oper_table[i]=oper[i];
}
for(i=0; i<4; i++) calculate(oper_order[i]);
cal_table[0]=rev(cal_table[0]);//기존과 동일
if(cal_table[0].d==1 && cal_table[0].u>0 && cal_table[0].u<=193){
for(i=0; i<5; i++) checklist[cal_table[0].u][i]=number[i];
for(i=5; i<9; i++) checklist[cal_table[0].u][i]=oper[i-5];
for(i=9; i<13; i++) checklist[cal_table[0].u][i]=oper_order[i-9];
}//결과값이 1~193 사이이면 해당하는 checklist에 표시해준다.
}
isBreak=next_permutation(number,number+5);
if(isBreak==0) break;
}//기존 코드에서의 반복문이 종료되었다. 이제 checklist에 기록된 정보를 눈으로 볼 수 있는 수식으로 시각화할 것이다.
for(i=1; i<=193; i++){
for(j=0; j<60; j++) canvas[j]=0;
for(j=0; j<5; j++) canvas[6*(2*j+1)]=checklist[i][j];
for(j=0; j<4; j++) canvas[6*(2*j+2)]=-checklist[i][j+5]-1;
for(j=0; j<5; j++){
group[j][0]=6*(2*j+1)-1;
group[j][1]=6*(2*j+1)+1;
}//캔버스를 비워준 뒤, 숫자와 연산자를 넣는다. +는-1, -는-2, *는-3, /는-4로 표시된다, 괄호가 들어갈 자리가 있게 5칸씩의 공백을 남겨준다.
for(j=0; j<4; j++){
order=checklist[i][j+9];
canvas[group[order][0]]=-5;
canvas[group[order+1][1]]=-6;
group[order][0]--;
group[order][1]=group[order+1][1]+1;
for(k=order+1; k<4; k++){
group[k][0]=group[k+1][0];
group[k][1]=group[k+1][1];
}
}//연산순서에 맞게 괄호로 수들을 묶어주는 코드이다.
printf("%d = ",i);
for(j=0; j<60; j++){
if(canvas[j]>0) printf("%d",canvas[j]);
if(canvas[j]==-1) printf("+",canvas[j]);
if(canvas[j]==-2) printf("-",canvas[j]);
if(canvas[j]==-3) printf("*",canvas[j]);
if(canvas[j]==-4) printf("/",canvas[j]);
if(canvas[j]==-5) printf("(",canvas[j]);
if(canvas[j]==-6) printf(")",canvas[j]);
}
printf("\n");//캔버스를 앞에서부터 읽으면서 해당하는 문자로 출력해준다.
}
}이 프로그램을 실행하면 4,5,6,7,8로 1~192사이의 수를 어떤 방법으로 만들 수 있는지 출력한다.
1 = ((8+7)/(6+(5+4)))
2 = ((8/((7-6)-5))+4)
3 = ((((8-7)-6)/5)+4)
4 = (8/(7-(6-(5-4))))
5 = ((8/(7+(6-5)))+4)
6 = ((((8*7)-6)/5)-4)
7 = ((8/(7-6))-(5-4))
8 = (8/(7/(6+(5-4))))
9 = ((8/(7-6))+(5-4))
10 = (8/((7-6)/(5/4)))
11 = (8+((7/(6-5))-4))
12 = (((8/(7-6))-5)*4)
13 = (8+(7-((6+4)/5)))
14 = (8*((7/(6-5))/4))
15 = ((8-7)*(6+(5+4)))
16 = (8*(7-(6-(5-4))))
17 = ((8/(7-6))+(5+4))
18 = (8*(7-(6-(5/4))))
19 = (8+((7/(6-5))+4))
20 = (8+(7+(6-(5-4))))
21 = (8+(7+(6/(5-4))))
22 = (((8*7)-(6*5))-4)
23 = ((8*(7/(6-4)))-5)
24 = (8*((7/(6-5))-4))
25 = (((8+7)*(6-4))-5)
26 = ((8-7)*((6*5)-4))
27 = (8-(7-((6*5)-4)))
28 = ((8/(7-6))+(5*4))
29 = (8-(7*((6-5)-4)))
30 = ((8*7)-((6*5)-4))
31 = (((8-(7-6))*5)-4)
32 = (8*(7+((6-5)-4)))
33 = ((8*(7/(6-4)))+5)
34 = (8*(7-((6+5)/4)))
35 = (8-((7-(6*5))-4))
36 = ((8/((7-6)/5))-4)
37 = ((8/((7-6)/4))+5)
38 = (8*(((6-7)/4)+5))
39 = (((8-(7-6))*5)+4)
40 = (((8*7)-6)/(5/4))
41 = ((((8*7)-6)-5)-4)
42 = ((8*7)+(6-(5*4)))
43 = (8+(7*(6-(5-4))))
44 = ((8/((7-6)/5))+4)
45 = (8-(7-((6+5)*4)))
46 = ((8*7)-((6-4)*5))
47 = (8+((7*4)+(6+5)))
48 = (8/((7/6)-(5-4)))
49 = (((8*7)-6)-(5-4))
50 = ((8*7)-(6/(5-4)))
51 = ((8*7)-(6-(5-4)))
52 = (((8/(7-6))+5)*4)
53 = ((8*7)+((6-5)-4))
54 = (8*(7-((6-5)/4)))
55 = (8-(7-(6*(5+4))))
56 = ((8+(7-(6-5)))*4)
57 = (8+(7*(6+(5-4))))
58 = (8*(7+((6-5)/4)))
59 = ((8*7)-((6-5)-4))
60 = ((8*(7/(6-5)))+4)
61 = ((8*7)+(6-(5-4)))
62 = ((8*7)+(6/(5-4)))
63 = ((8*7)+(6+(5-4)))
64 = ((8+(7+(6-5)))*4)
65 = ((8+(7-(6-4)))*5)
66 = (8*(((7+6)/4)+5))
67 = ((8*(7+(6-4)))-5)
68 = ((8*(7+(6-5)))+4)
69 = (8+(((7+6)*5)-4))
70 = ((8*7)-(6-(5*4)))
71 = ((8*7)+(6+(5+4)))
72 = (8/((7-6)/(5+4)))
73 = ((8*(7+(6/4)))+5)
74 = (8*(((7*6)-5)/4))
75 = ((8+7)*(6-(5-4)))
76 = (8*(7+(5/(6-4))))
77 = (8+(((7+6)*5)+4))
78 = (8*(7+((6+5)/4)))
79 = ((8*(7*(6/4)))-5)
80 = (8*(7-((6-5)-4)))
81 = ((((8+7)*6)-5)-4)
82 = ((8*7)+((6*5)-4))
83 = (8+((7*(6+4))+5))
84 = (8*(7/(6/(5+4))))
85 = ((8*7)+((6*4)+5))
86 = (((8*(7+5))-6)-4)
87 = ((8*(7+4))-(6-5))
88 = (8*((7/(6-5))+4))
89 = (((8+7)*6)-(5-4))
90 = ((8*7)+((6*5)+4))
91 = (((8+7)*6)+(5-4))
92 = ((8*((7-5)*6))-4)
93 = (8-((7-(6*4))*5))
94 = (8*(((7*6)+5)/4))
95 = (((8*(7+6))-5)-4)
96 = (8*(7+(6-(5-4))))
97 = (((8+6)*7)-(5-4))
98 = ((8*(7+5))+(6-4))
99 = (((8+7)*6)+(5+4))
100 = ((8*7)+((6+5)*4))
101 = (((8+(7+6))*5)-4)
102 = ((8+7)*(6+(4/5)))
103 = ((8*(7+6))-(5-4))
104 = (((8*7)-(6*5))*4)
105 = ((8*(7+6))+(5-4))
106 = (8-(7*(6-(5*4))))
107 = ((8*(7*(6-4)))-5)
108 = (8*(7+((6/4)+5)))
109 = (((8+(7+6))*5)+4)
110 = ((8*7)+(6*(5+4)))
111 = ((8*6)+(7*(5+4)))
112 = (8*(7+(6+(5-4))))
113 = ((8*(7+6))+(5+4))
114 = (8*(7+(6+(5/4))))
115 = (((8*(6-4))+7)*5)
116 = (8*(7+(6*(5/4))))
117 = ((8*(7*(6-4)))+5)
118 = (8*((7*(5/4))+6))
119 = (((8+(7+4))*6)+5)
120 = ((8-7)*(6*(5*4)))
121 = (8-(7-(6*(5*4))))
122 = (((8*7)+5)*(6-4))
123 = (((8+5)*(6+4))-7)
124 = ((8*(7+6))+(5*4))
125 = (8+((7+6)*(5+4)))
126 = ((8-(7-(5*4)))*6)
127 = ((8*(6+(5+4)))+7)
128 = (8*(((7-5)*6)+4))
129 = (((8+7)*(5+4))-6)
130 = (8*((7+6)*(5/4)))
131 = ((8*(7+(6+4)))-5)
132 = (((7*5)-(8-6))*4)
133 = (((8+6)*(5+4))+7)
134 = ((8*(7+(5+4)))+6)
135 = (8+(7+(6*(5*4))))
136 = (8*(7+((6-4)*5)))
137 = (((8+(6+5))*7)+4)
138 = ((8+((7-4)*5))*6)
139 = ((8*((7-4)*6))-5)
140 = ((8*(7+(6+5)))-4)
141 = ((8*(7+(6+4)))+5)
142 = (8+((7*(5*4))-6))
143 = ((((8*5)-6)*4)+7)
144 = (8*((7+5)*(6/4)))
145 = (((8+7)*(6+4))-5)
146 = (8+(((7*4)-5)*6))
147 = (((8*(6-4))+5)*7)
148 = ((8*(7+(6+5)))+4)
149 = ((8*((7-4)*6))+5)
150 = ((8+7)*((6-4)*5))
151 = (((8+4)*(7+6))-5)
152 = (8*((7*(6-4))+5))
153 = (((8+(6*4))*5)-7)
154 = (8*(7*((6+5)/4)))
155 = (((8+7)*(6+4))+5)
156 = (8+(((7*6)-5)*4))
157 = ((8*(6*4))-(7*5))
158 = ((7*((6*5)-8))+4)
159 = ((((8*6)-7)*4)-5)
160 = (8/(((7-6)/5)/4))
161 = (((8+7)*(6+5))-4)
162 = ((((8-4)*5)+7)*6)
163 = (8+((7+(6*4))*5))
164 = (((8+6)*(7+5))-4)
165 = ((((8*6)-5)*4)-7)
166 = (((8+(7*5))*4)-6)
167 = (((8+(6*4))*5)+7)
168 = (8*(7-(6-(5*4))))
169 = (((8+7)*(6+5))+4)
170 = (8+((7+(5*4))*6))
171 = (8+((7*(6*4))-5))
172 = (8+(((7*5)+6)*4))
173 = (((8+5)*(7+6))+4)
174 = (((8*(7-4))+5)*6)
175 = (((8+(5*4))*6)+7)
176 = (8*((7*6)-(5*4)))
177 = ((((8*5)+6)*4)-7)
178 = (((8+(7*5))*4)+6)
179 = ((((8*6)-5)*4)+7)
180 = ((((8*7)-6)-5)*4)
181 = (8+((7*(6*4))+5))
182 = ((8+6)*((5*4)-7))
183 = ((((8*4)+6)*5)-7)
184 = (8*(((7-4)*6)+5))
185 = ((((8*6)-7)-4)*5)
186 = (((8+(7*4))*5)+6)
187 = ((((8*4)-6)*7)+5)
188 = ((8*6)+(7*(5*4)))
189 = ((8+(7+6))*(5+4))
190 = (8+(7*((6*5)-4)))
191 = ((((8*5)+6)*4)+7)
192 = (8*((7-(6-5))*4))
193 = ((((+)+)+)+)신기한 사실은, 1~192의 모든 수를 나누기 없이 만들 수 있다는 것이다! 궁금하면 직접 코드를 수정해서 해 보시길!
for(oper[0]=0; oper[0]<4; oper[0]++).. 가 써져 있는 부분에서 4를 3으로 바꾸면 된다! (나누기가 3을 의미하므로)
결론: 1부터 연속한 자연수를 가장 많이 만들 수 있는 방법은 4,5,6,7,8을 고르는 것이며, 이는 1~192의 모든 수를 만들 수 있다.
-
아, 제가 처음부터 문제 이해를 잘못했네요... 아무거나 선택해서 최대로 만드는게 아니구나...
-
코딩 열풍이 불어닥친 것 같아요! 문제를 출제한 백진언 연구원 님의 코멘트를 전달할테니 참고하세요!!!
1번 문제
친구들의 풀이가 모두 의미 있었어요. 친구들의 예상과 달리 1번의 답은 '존재한다'고, 나눗셈을 이용해 정수 뿐만이 아니라 유리수까지 다뤄야 한다는 것이 키 포인트였습니다!
2번 문제
2번 문제는 컴퓨터의 도움 없이는 해결이 힘든 문제였어요. muse, 누군가, 수돌이 친구가 프로그래밍을 이용해 문제에 접근했는데요, 다들 프로그램을 잘 이용했습니다.
프로그래밍으로 문제를 풀 때 단점은, 문제 오류가 아닌 프로그램밍 자체를 실수하면 답에 오류가 생길 수 있습니다. 그래서 수학 문제를 프로그래밍으로 해결할 때는 다른 사람이 프로그램을 제대로 구현했는지 확인해서 '엄밀함'을 검증할 수 있습니다. 더 좋은 방법은 다른 방식으로 구현한 프로그램도 똑같은 답을 주는 지를 확인하는 거예요.
수돌이 친구가 2번 문제를 프로그래밍으로 해결했지만, 수돌이 친구의 코드가 맞는지 다른 사람이 확인하지 않았기 때문에, 다른 친구들이 ①수돌이 친구의 구현을 검증해서 확인하거나 ②새로 구현을 해서 똑같은 답이 나오는지를 확인하면 문제를 완전히 해결한 걸로 하겠습니다.
문제를 생각한 친구들 전부 수고 많았고, 아직 할 일이 남았으니 조금만 더 힘내시길 바라요. 감사합니다!
-
따로 새롭게 구현하여 보았습니다. 역시 똑같은 답 "192 for (4, 5, 6, 7, 8)"이군요.
소스 코드: /resources/comment/2018/09/d99406d8b87e238aa15b6f172454a0cc.cpp
실행 결과(output.txt, 크기 약 31KB): /resources/comment/2018/09/32cd71ab0102d2f22dc991c2bb6d7cc0.txt
전체 경우를 따져보는 방식을 조금 바꾸어, 확인해야 하는 경우의 수를 조금 줄였습니다. 이 코드에서는 그것이 362,797,056에서 300,231,360으로 줄어든 정도이긴 합니다만, 같은 수가 있는 경우를 더 처리한다면 1.5억(150,000,000) 정도까지, 혹은 더 줄일 수 있을 것 같습니다.
경우의 수를 줄인 기본적인 아이디어는, 덧셈과 곱셈의 결합법칙이 성립한다는 데서 나왔습니다. 120가지 permutation에 대해 24가지 순서를 해 보는 대신, 5개 중 먼저 연산할 2개를 고르고, 나머지 4개 중 2개를 고르는 식으로 바꾸면, 120*24를 180으로 바꿀 수 있습니다. 대신, 뺄셈과 나눗셈은 연산의 순서를 고려해야 하므로, 연산의 종류가 4가 아닌 6이 됩니다. 5개의 수가 모두 다른 경우 경우의 수가 120*24*4^4=737,280에서 180*6^4=233,280으로 줄어듭니다. 따져봐야 할 경우가 1/3 정도로 줄어든다는 거죠.
※ 트리비아
1. (4, 5, 6, 7, 8) 다음으로 좋은 조합은 (2, 4, 7, 8, 9)로, 180까지 나타낼 수 있습니다. 1등(192)과의 격차는 좀 크군요.
2. 문제의 "1 이상, 9 이하"를 "1 이상 10 이하"로 바꿀 경우 답은 "210 for (2, 3, 7, 9, 10)"입니다. 10을 포함하는 경우 (4, 5, 6, 7, 8)은 전체에서 4등입니다.
3. (1, 2, 3, 4, 5)로 연속해서 만들 수 있는 수는 75가 한계입니다(541등). 다른 댓글에서 (3, 4, 5, 7, 9)가 있었는데, (3, 4, 5, 7, 9)는 144까지를 만들 수 있는, 1287개 중 39등인 조합입니다.
4. (1, 1, 1, 1, 1)보다 더 안 좋은 경우가 있을까요? 있습니다! (8, 8, 8, 9, 9)와 (8, 8, 9, 9, 9)가 그 주인공입니다. 이 둘은 5를 나타낼 수 없습니다.
5. 같은 수 5개를 쓴다면, 1부터 9 중에서는 4가 그나마 낫습니다. (4, 4, 4, 4, 4)는 1부터 21까지의 수를 나타낼 수 있습니다.
-
아 늦었네요... 답은 똑같습니다.
https://scratch.mit.edu/projects/247868405/
1~9로 만들 수 있는 중복조합리스트를 미리 뽑아놓고 숫자 배열까지 생각하여 계산하였습니다.
-
-
근데요, 폴리매스가 원래(매스펀도 그렇고) 중간에 갑툭튀한 분이 정답을 맞히는 경우가 많나요? 보니깐 그런 경우 되게 많던데.
-
-
??? 수학장님 수학동아 폴리매스에서 알만한 사람 다 아는 top3(여백 패르마,구머,수학장)로 알고 있었는데, 지금까지 멘토링을 못 받았나요?
좋아요0 -
여백 패르마님도 아직 멘토링 안 받아보셨답니다.... 구머님은 받으셨나 문제 플어야 멘토링이 되서 멘토링 받은 분들은 별로 없어요 연락이 안 되서 못 받은 분들도 계시고 수돌이님,c언어님같은 예전 멤버분들이 멤토링 받으신 적 있어요
좋아요0 -
저도 스케줄 문제땜에 아직 받은 적 없습니다
좋아요0 -
그리고 이제는 top 3는 아니죠....학교일 바빠서 접은지 거의 4달이 된 것 같은데 ㅜㅜ
좋아요0 -
맞아요.... 그리고 제가 1,2번 문제는 가끔 풀어도 메인 문제는 한 번도 푼 적이 없어요ㅠㅠ 제가 무슨 top3입니까
좋아요0 -
음... 그런가요...(그럼 예전 top3였나...)
좋아요0
-
-
-