21번째 문제는
KPP 멤버 '한동규' 님이 만든 문제입니다
무한한 크기의 체스판에 '나이트' 유한개를 배치하려고 한다. 아래 각각의 조건에 대해 배치가 가능하다면 그 예시를 찾고, 불가능하다면 이유를 설명해 보자. (단, 나이트의 색은 무시해도 된다.)
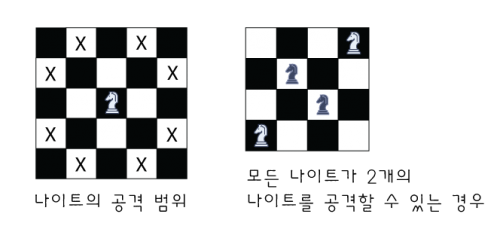
조건1. 모든 나이트가 각각 3개의 나이트를 공격해야 한다.
조건2. 모든 나이트가 각각 4개의 나이트를 공격해야 한다.
조건3. 모든 나이트가 각각 5개의 나이트를 공격해야 한다.
★주의 사항★
정답과 풀이는 비밀 댓글로 부탁드려요!
이름, 주소, 연락처를 함께 남겨주세요!
당첨자는 수학동아 10월호에 공개합니다!
풀이는 9월 25일 이후 이 게시물에서 확인하세요!
*KPP (Korean Puzzle Party)는 '퍼즐을 좋아하는 사람들의 모임'으로 퍼즐을 모으는 사람, 퍼즐을 만드는 사람, 퍼즐을 푸는 사람들이 모여 직접 만들고 수집한 퍼즐을 함께 풀어보며 이야기를 나눈다. 현재 두 달에 한 번 서울에서 정기적인 모임을 갖고 있으며, 퍼즐을 푸는 것뿐 아니라 퍼즐 관련 행사에 참여하거나 박물관에 다녀오는 등 다양한 활동을 하고 있다.
스크롤 주의!
아래 정답이 있습니다!
.
.
.
.
정답과 해설
서로 공격하는 나이트끼리 선으로 이은 연결 구조(그래프)를 생각하자. (1)번 문제의 경우 각 나이트에서 뻗어나가는 선이 3개여야 한다. 이러한 연결 구조를 가진 예시 중에는 정육면체가 있다. 그림과 같이 정육면체를 평면에 사영시킨 모양은 조건을 만족하므로 답이 된다.
(2)번 문제도 마찬가지로 초입방체를 평면에 사영시킨 모양이 답이 된다. 참고로 두 문제 모두 소개한 배치 외에도 수많은 답이 존재한다.
(3)번 문제의 경우 다음과 같이 불가능함을 증명할 수 있다. 조건을 만족하는 나이트의 배치가 존재한다고 가정하자. 나이트의 수가 유한하므로 나이트 배열의 가장 윗줄에 있는 나이트를 생각할 수 있다. 가장 윗줄의 나이트 위에는 다른 나이트가 존재하지 않아야 하므로 이 나이트가 다른 나이트를 공격할 수 있는 칸은 여덟 칸 중 아래 네 칸 뿐이다. 하지만 모든 나이트가 다섯 개의 나이트를 공격해야 한다는 조건에 모순된다. 따라서 조건을 만족하는 나이트의 배치는 존재하지 않는다.
-끝-











