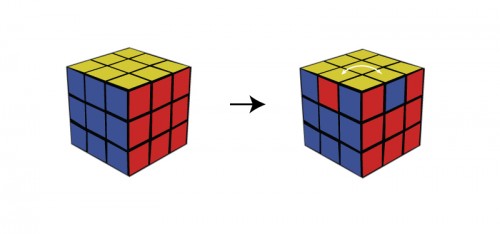
문제 3X3X3 루빅스 큐브를 생각하자. 아래 그림처럼 두 조각을 뽑아 위치를 바꿔 끼우면 큐브를 회전시켜서 원래 모양으로 만들 수 있을까?
-
꼭짓블럭을 바꿔 끼면 가능한데 엣지 두개가 바뀌는 것은
4x4x4로 확장시켜서 풀면 편할 것 같은데?
-
4*4*4 큐브로 바꿀 수 없는 한 불가능합니다.
-
조각이 아닌 면 하나 하나로 구분해서, 꼭짓점 조각과 중앙 조각의 면을 제외하면 24개의 면이 있습니다(즉 모서리의 면 조각들입니다).
이 면들은 위치가 다르더라도 색깔이 같으면 변하지 않는것으로 봅니다.
이때 한 면을 변화시키기 위한 방법은 한가지입니다(큐브를 돌리는 경우, 면을 포함하는 돌림이 2가지 존재하지만, 하나는 색깔이 변하지 않음).
또한 한번 돌릴때마다 4개의 면이 바뀌게 됩니다.
즉 바뀐 면의 갯수는 0개 혹은 4의 배수로 일정합니다.
위와같은 경우는 2개가 바뀌어 있으므로 불가능합니다.
-
한 면을 변화시킬 수 있는 방법이 2가지이네요. 다시 정리 해서 올리겠습니다.
좋아요1 -
제가 잠시 착각했네요.
면 하나 하나로 구분해, 꼭짓점조각과 중앙조각을 제외한 24개의면을 중점으로 봅니다.
각각의 면에 중앙조각과 색이 같다면 1, 다르다면 0를 부여합니다.
이 합들을 cube-sum이라 정의합니다.
이때 중앙조각은 돌아가지않는것으로 보는데,
큐브 전체에서 중앙부분을 돌리는것은 그 양사이드의 면을 돌리는것과 같기 때문입니다.
즉 면을 돌리는 것은 사이드면만 보아도 무방합니다.
면을 한 번 돌리게 되면 8개의 면의 위치가 바뀌게 되는데, 중앙조각과 같은 면에 존재하는 (작은)면은 색이 중앙조각과 여전히 같으므로 4개의 면을 바꿀 수 있습니다.
또한 한 면의 입장에서 위치를 바꿀 수 있는 경우는 2가지이나, 같은 면에 존재하는 중앙조각의 돌림의 경우는 중앙조각과의 색 관계가 여전히 같으므로
한 면을 바꿀 수 있는 돌림은 한 가지 뿐입니다.
종합하면, 한 번 돌릴때마다 4개의 면을 바꿀 수 있고 면마다 바꿀 수 있는 경우는 단 1가지밖에 존재하지 않기때문에
cube-sum은 4의배수가 됩니다.
위의경우는 cube-sum이 22로 4의 배수가 아니기 때문에
불가능합니다.
좋아요0
-
-
-
-
-
훌수*훌수*훌수 큐브는 3개 이상에 조각이 규칙적 변화하기 때문에 두조각만 바꾸면 원래 모양으로 만들수 없습니다.
-
-
-
-
안되는 건 알겠는데 증명을 어떻게 해야할지...
-
확인요청중
https://www.youtube.com/watch?v=o-RxLzRe2YE
여기에 이 문제에 대한 답이 있내요.
-
-
확인요청중
처음 써보는데 양해부탁드립니다. :)
큐브에서 1회전을 할 경우에 엣지4개 (모서리 부분 조각)와 코너4개 (꼭짓점 부분 조각)의 위치가 바뀝니다.
문제에서는 엣지의 위치가 바뀌었음으로 엣지를 먼저 고려하겠습니다.
A,B,C,D
각각의 조각에 위와같이 이름을 붙인뒤, 1회전을 하였을때
D,A,B,C
이렇게 바뀝니다.
이는 조각 2개간의 교환을 3번한것과 같습니다.
A,B,C,D -> A,B,D,C -> A,D,B,C -> D,A,B,C
2회전을 한다면
A,B,C,D -> A,B,D,C -> A,D,B,C -> D,A,B,C -> D,A,C,B -> D,C,A,B -> C,D,A,B
이렇게 6번의 교환을 거칩니다.
루빅스 큐브는 어떻게 회전에도 그 회전의 모양은 같기 때문에
1회전 = 3교환
2회전 = 6교환 이 되며, 이는
(홀수)회전 = (홀수)교환
(짝수)회전 = (짝수)교환 을 나타냅니다.
그렇기에 홀수번 교환한 상황에서는 홀수번으로만 해결 할 수 있고
짝수번 교환한 상황에서는 짝수번으로만 해결 할 수 있습니다.
코너 조각도 위와 마찬가지입니다.
정리하면 큐브를 섞을시에는
1. 홀수회전 시에는 홀수번의 교환이 있다.
2. 짝수회전 시에는 짝수번의 교환이 있다.
3. 엣지와 코너조각은 1회전시 항상 4조각씩 같이 움직이기 때문에
엣지와 코너조각의 교환횟수는 짝수 or 홀수로 같아야한다.
(1회전 시에는 엣지 3번, 코너3번으로 위의 조건을 만족합니다. 2회전도 마찬가지구요.)
하지만 문제의 상황을 보면 엣지의 교환횟수는 1번, 코너의 교환횟수는 0번(다 맞춰져 있음으로) 입니다.
이는 3번 정리와 모순됨으로, 문제의 상황은 맞출 수 없는 상황입니다.
-
확인요청중비밀 댓글이 등록 되었습니다.댓글 작성하기 댓글수0