퍼즐파티
재밌는 수학 퍼즐과 퀴즈가 한가득!
[킹앤카&킹앤포&킹앤유] [포7] 눈물의 졸업파티 퀴즈 1번 풀이
2월호 킹앤포 퀴즈1번 답의 좀더 상세한 풀이를 공개합니다!
먼저 이웃한 자리의 개념부터 살펴보겠습니다.
각 자리에 1부터 12까지 숫자를 매기고 이웃한 자리를 피하려면 얼마나 차이나야 하는지 봅시다.
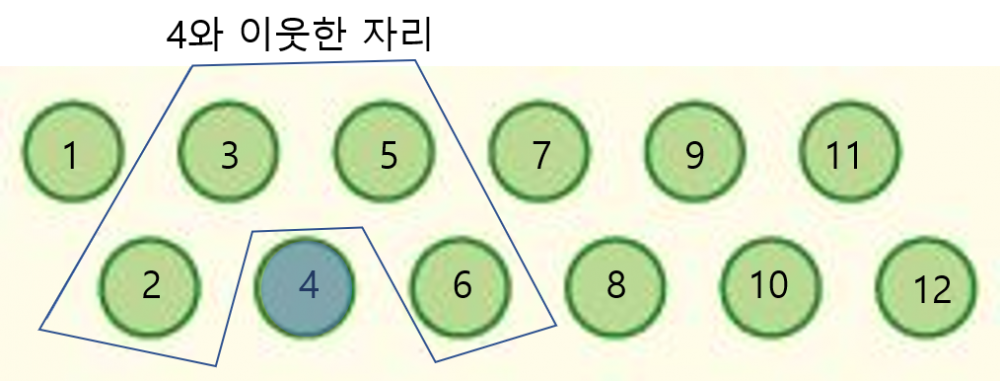
위 그림처럼 4번에 섰다면 4와 이웃한 자리는 2,3,5,6이 됩니다. 그러니 자리를 1~12로 매기고 일렬로 나열했다고 했을 때 이웃하지 않으려면 적어도 2 이상 차이나야 합니다. 따라서 A, B, C가 설 자리를 #이라고 하고 그 사이에 꼭 들어가야할 자리를 *이라고 하면 최소 조건을 만족하는 배치는 # * * # * * #입니다.
그러면 남은 좌석 수는 5(=12-3-4)이고, 이 5자리는 # * * # * * #의 배치를 유지한 상태로 #으로 구분된 4영역에 배치돼야 합니다. 이 5자리를 4영역에 배치하는 방법의 수는 4H5=8C5=56이며, A, B, C 3명의 자리를 결정하는 경우의 수는 3!, 나머지 9명의 자리를 결정하는 경우의 수는 9!이므로 이 숫자를 모두 곱하면 전체 경우의 수를 구할 수 있습니다!
|
|
닫기










