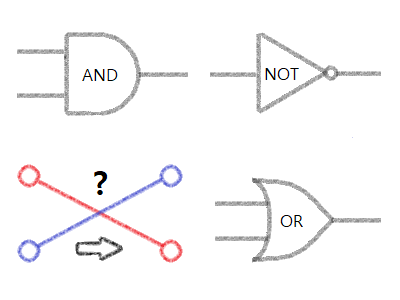
1) 직사각형의 왼쪽 두 꼭짓점이 입력 단자고, 오른쪽 두 꼭짓점이 출력 단자다. 배선끼리 교차하지 않으면서, 즉 끝점이 아닌 곳에서 만나지 않으면서 위아래가 바뀌어 출력되도록 해보자. 모든 회로는 직사각형 내부에 있어야 하고, AND, OR, NOT 게이트를 이용할 수 있다.
2) 위의 경우에서 XOR 게이트까지 이용하면 가능한가?
잘못된 표현 등은 지적해주시면 감사하겠습니다.
+ 정확성을 위해 추가해야 할 것이 있어 수정했습니다.
- 각 게이트는 사용하지 않거나 중복해서 사용해도 되며 사용 개수에는 제한이 없습니다. 직사각형 내부에만 들어가 있으면 됩니다.
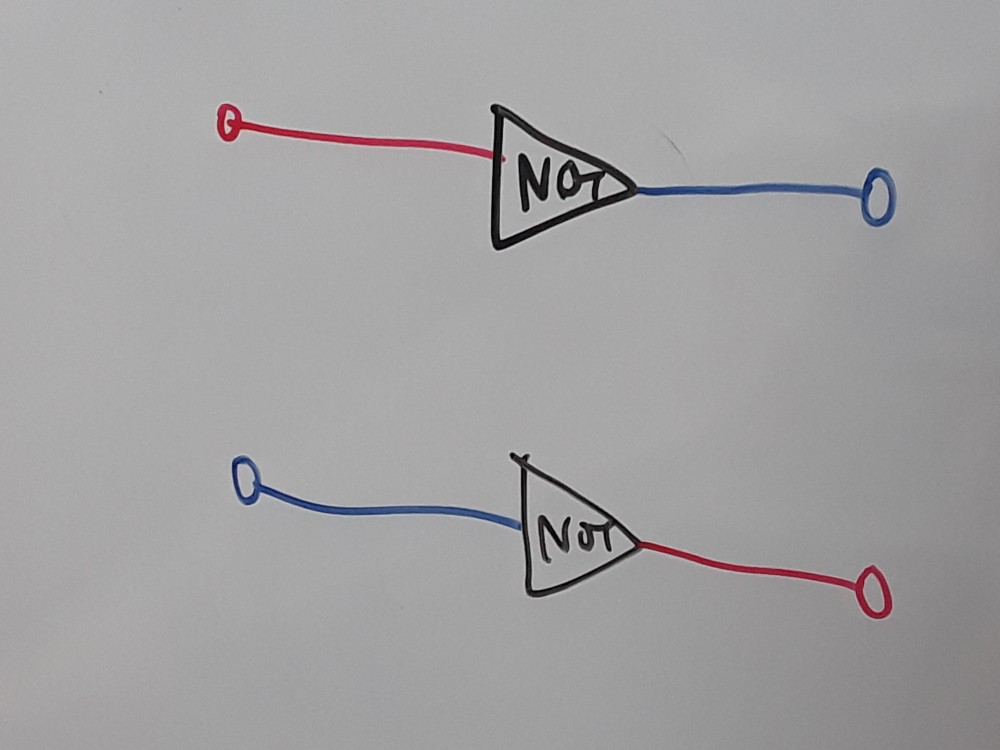
- 문제의 빨간색, 파란색은 ON/OFF를 나타내는 것이 아니라 두 입력이 어떻게 출력되는지 나타낸 것인데, 오해가 있었다면 죄송합니다.
- 한 단자에서 여러 배선이 시작되거나, 여러 배선이 한 단자로 모이는 경우는 끝점에서 만나므로 교차한 것으로 생각하지 않습니다.
좋아요
0
글쎄요
0
어려워요
0
-
근데 각 게이트를 2번 이상 사용 불가능하죠? 만약 가능하면 그냥 직선으로 이은 다음 NOT게이트 2개 사용하면 되는데...
-
아니죠 위아래 인풋이 같으면 안 되잖아요
좋아요0 -
그래서 결국에는 서로에 관련되게 코드를 짜야해서 같은 회로에서 만날 수 밖에 없을 것 같은데
좋아요0 -
그러니까 제 말은 이렇게요.
 좋아요0
좋아요0 -
그러니까 위도 1, 밑에도 1이면 output이 0,0이 되잖아요.
문제는 1번 인풋이 2번 아웃풋이 되게, 2번 인풋이 1번 아웃풋이 되게 만드는 게 목적이예요.
좋아요0 -
제 생각에는 2개의 인풋을 1개의 논리회로에 엮으면 그림상으로 만나지 않으니까 교차하는게 아니라고 하는 그런 식 아닐까요?
그게 아니면 절대로 할 수 없을 것 같은데...
좋아요0 -
아 위아래 인풋이 같아도 됐군요...
좋아요0 -
Horizontal 님이 말씀하신 대로 끝점(단자)에서 만나는 경우는 교차로 간주하지 않습니다. 문제에도 그 내용을 추가할게요~
좋아요0
-
-
다시 도전
-
미리 말씀드려야 했는데, 이 문제는 저도 답을 모릅니다. 다같이 생각해보기 위해 올렸어요!
-
불가능하다도 답이 될 수 있나요? (아직 확신은 안 서지만 만약 1번이 가능하면 2번은 자동으로 가능해져서요.)
-
다시 도전
-
NOT을 아래가 아니라 위에 연결하는 것으로 수정하겠습니다.
좋아요0 -
비밀 댓글이 등록 되었습니다!
-
만약 그렇다면 제 생각에는 불가능할 것 같습니다. 적어도 2개 이상의 AND 또는 OR을 써야 할텐데 그러면 반드시 선이 교차하게 될 것 같네요 ㅇㅅㅇ (그냥 추측입니다)
좋아요0 -
혹시 논리회로를 어디서 배웠는지 여쭤봐도 될까요? 저는 혼자 인터넷 보고 공부했는데 인터넷으로는 한계가 있는 것 같아서...
좋아요0 -
- 여기에 다신 비밀 대댓글은 저한테는 보이지 않네요. 혹시 제 댓글 중 아무거나에 다시 비밀 댓글로 달아주실 수 있나요?
- 저도 논리회로에 대해 따로 배운 것은 아니고, 리프님처럼 인터넷에서 검색을 하여 알게 되었습니다. 그러던 중 이러한 의문이 들게 되어 문제로 만들었고요. 그래서 이 문제에도 오류나 부족한 점이 있을 수도 있습니다.
좋아요0 -
별 특별한 내용은 없어서 그냥 공개댓글로 바꿨습니다.
좋아요0
-
-
- 알립니다 -
조사를 통해 이 문제에 대한 연구 결과를 찾을 수 있었습니다. 입력의 위아래가 바뀌어 출력되는 것을 'crossover'이라고 부르더군요. 2)의 해답을 먼저 말한 후 1)을 서술하는 것이 자연스러우므로 그렇게 하겠습니다.
2) 아래의 그림처럼 하면 XOR 게이트만을 이용해 crossover을 할 수 있습니다.
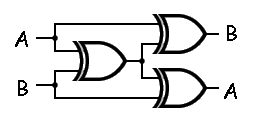
(출처: https://en.wikipedia.org/wiki/Nobili_cellular_automata)
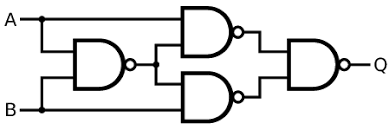
1) 아래의 그림은 NAND 게이트를 이용해 XOR 게이트를 구현한 것입니다. 그런데 NAND게이트는 단순히 AND와 NOT의 결합에 불과하므로, XOR 게이트를 이 두 게이트만으로 만들어낼 수 있다는 뜻입니다. 마지막으로, 이 AND와 NOT으로 구현한 XOR 게이트를 1)에 대입하면 그 두 종류의 게이트만으로 crossover이 일어난다는 것을 알 수 있습니다.