함께 풀고 싶은 문제
창의력을 기를 수 있는 수학 문제 또는 퍼즐을 내는 곳입니다.
삼차방정식 근의 공식은
삼차방정식 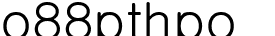 =0에서의 근을
=0에서의 근을 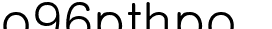 ,
, 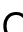 ,
, 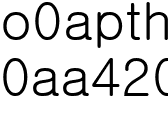 라 할 때,
라 할 때,
![-\frac{1}{3a}\sqrt[3]{\frac{2b^{3}-9abc+27a^{2}b+\sqrt{(2b^{3}-9abc+27a^{2}b)^{2}-4(b^{2}-3ac)^{3}}}{2}}](http://www.polymath.co.kr/resources/latex/b5b42a84d1154a2a00a412b49122d303.gif)
![-\frac{1}{3a}\sqrt[3]{\frac{2b^{3}-9abc+27a^{2}b-\sqrt{(2b^{3}-9abc+27a^{2}b)^{2}-4(b^{2}-3ac)^{3}}}{2}}](http://www.polymath.co.kr/resources/latex/ff72c47aaf60d62ce59948b857826686.gif)
![+\frac{1+i\sqrt{3}}{6a}\sqrt[3]{\frac{2b^{3}-9abc+27a^{2}b+\sqrt{(2b^{3}-9abc+27a^{2}b)^{2}-4(b^{2}-3ac)^{3}}}{2}}](http://www.polymath.co.kr/resources/latex/d384cb5be4f77b5ffbd5fddb5a429c20.gif)
![+\frac{1-i\sqrt{3}}{6a}\sqrt[3]{\frac{2b^{3}-9abc+27a^{2}b-\sqrt{(2b^{3}-9abc+27a^{2}b)^{2}-4(b^{2}-3ac)^{3}}}{2}}](http://www.polymath.co.kr/resources/latex/018c194ae20bcfe2ba35935410fd3a2c.gif)
![+\frac{1-i\sqrt{3}}{6a}\sqrt[3]{\frac{2b^{3}-9abc+27a^{2}b+\sqrt{(2b^{3}-9abc+27a^{2}b)^{2}-4(b^{2}-3ac)^{3}}}{2}}](http://www.polymath.co.kr/resources/latex/ca23dead267e4b1496f760dc1834c73f.gif)
![+\frac{1+i\sqrt{3}}{6a}\sqrt[3]{\frac{2b^{3}-9abc+27a^{2}b-\sqrt{(2b^{3}-9abc+27a^{2}b)^{2}-4(b^{2}-3ac)^{3}}}{2}}](http://www.polymath.co.kr/resources/latex/61039458cecb4824cd1abbe14ac8ade5.gif)
이다.
왜 그럴까?
이 문제 어떠셨나요?
좋아요
0
글쎄요
0
어려워요
0
닫기











