KASIT 수학문제연구회 학생들이 출제한 수리 논술 문제입니다. 문제를 잘 풀어준 학생을 뽑아 수학문제연구회 학생들이 직접 답안을 첨삭해줄 예정입니다. 문제를 풀어 보세요!
어은동산을 선책하던 성연이는 수상한 종이 한 장을 발견한다. 알고 보니 보물지도가 아닌가! 보물지도는 다음과 같다.
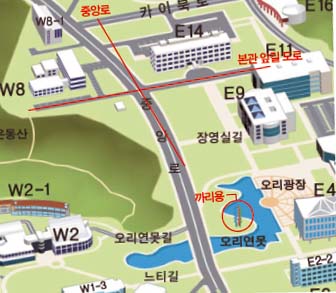
보물은 중앙로와 본관 앞길 도로에서 같은 거리만큼 떨어져 있으며 까리용에서 1000m만큼 떨어진 곳에 묻혀있다.
성연이는 고민하다 잘 풀리지 않아 수학문제연구회 친구들과 함께 보물을 찾아보기로 했다. 친구들이 파야 할 장소는 몇 군데일까? 단, 중앙로와 본관 앞길 도로 모두 직선이라 가정한다.
-
죄송합니다, 4군데는 아닌것같군요.
도로 2개의 교차점에 원의 중심을 잡고 원을 그립니다.
그러면 반지름의 길이가 정해지지 않았으므로, 수없이 많이 나오게 되겠죠?
그리고 까리용에도 원의 중심을 잡아 원을 그립니다.
1000m가 어디인지 모르기때문에 두 원의 반지름을 아무렇게 잡아주면 두 원의 교차점은 최대로 2군데가 나오기때문에 파야할 곳은 2군데가 나옵니다.
오류 지적 감사합니다.
-
제 생각은 좀 다릅니다. 직선 2개가 교차하는 점에 원을 그린다고 꼭 두 직선에서의 거리가 똑같다고 보기는 힘들 것 같습니다. 제대로 본다면,
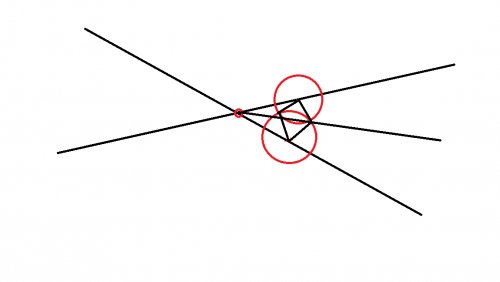
이런 꼴이 더 정확하겠지요(그림이 좀 허접하긴 한데, 빨간 점에서 원들 사이로 그은 직선은 두 원의 교점을 지나고, 두 원의 반지름은 같습니다). 거의 각이등분선에 가깝습니다.
그렇게 되면 빨간 점에서 그을 수 있는 직선 개수는 총합 2개가 됩니다. 이를 참고해봅시다.
1) 까리용과 까리용과 가장 거리가 최단인 직선의 한 부분의 거리가 1000m가 넘을 경우:
두 도로가 이루는 각에 따라서 아예 안 접할수도 있을 것이고, 최대 2군데에서 접하게 될 것입니다.
2) 딱 맞닿는 경우:
무조건 2군데에서 만납니다.
3) 1000m을 넘을 경우:
최소 2곳, 최대한 4군데에서 만나게 됩니다.그림을 그려서 보여드리려고 했는데 시간이 없네요. 나중에 보여드리겠습니다. 저도 틀린것이 있을 것 같으니 오류 지적 환영합니다.
좋아요0 -
제네릭/// 거의 각 이등분선이 아니라 그냥 각 이등분선이어야 두 도로 에서의 거리가 똑같다고 할 수 있습니다.
1에서 도로와 까리용의 거리가 1000m 가 넘는데 2군데에서 접한다는 부분이 이해가 안갑니다.....
밑에 그림에서 검은직선은 도로, 파란직선은 도로의 각 이등분선 , 점F는 까리용 입니다.
파란직선상의 모든 점은 두 도로에서 같은 거리에 있습니다. 그러므로 까리용에서 반지름이 1000m인 원을 그려 파란직선과 만나는 교점을 파면 보물을 찾을 수 있습니다.
저 지도에서 1000m가 어느정도인지 모르니 모든 경우를 따져 봅시다. 먼저 까리용이 각 이등분선위에 있지 않을 때(그림 상으로는 아무리 봐도 각 이등분선위에 있지 않긴하지만)
1)원이 어느 파란 직선과도 만나지 않는 경우
보물이 있는 곳이 없습니다. 보물지도가 가짜입니다.
2)한 직선과 접할경우
한 곳만 파보면 되겠네요
3)한 직선과 두 점에서 만날경우
2곳을 파면 됩니다.
4)한 직선과 두 점에서 만나고 다른 한 직선과 접할 경우
3곳
5)두 직선과 각각 두점에서 만나는 경우(약간 다른 두가지경우가 있습니다.
4곳
6)원이 두직선의 교점을 지날 경우
3곳
좋아요0 -
모든 경우를 한번에 나타내면
이렇게 됩니다.
정리하면 까리용을 중심으로 한 원과 두 도로의 각 이등분선이 만나지 않을 때 교점이 0개
한 직선과 접할 때 1개, 그 보다 원이 커지면 2,3,4개 까지 늘어나다가 원이 직선의 교점을 지날 때 3개 그 이후로는 계속 4개 입니다.
좋아요0 -
비슷한 원리로 까리용이 각 이등분선 위에 있을 때 원과 각 이등분선의 교점이 0개,2개,4개가 됩니다.
좋아요0 -
그렇군요. 제가 잘못 생각했습니다. 직선 도로 자체와 맞닿는 점 개수를 구해버렸네요.
좋아요0
-
-
저는 6군데 같습니다. 왜냐하면 좌표로 생각해보았을때 중앙로와 본관 앞길 도로에서 같은 거리에 있는 지점을 연결한 직선이 까리용에서 반지름1000미터로 그린 원과 만나는 지점을 생각 해 보면 1사분면과 2사분면에서는 1개씩 만날 수 있고 3사분면과 4사분면에서는 각각2개씩 만날 수 있기 때문입니다.










