국가수리과학연구소 35번
돌아온 보드게임 페스타!
문제 출제자 : 김종락 서강대학교 수학과 교수
*이번 달은 국가수리과학연구소 대신 김종락 서강대학교 수학과 교수님께서 문제를 출제해주셨습니다.
전 세계에는 아직 우리가 보지 못한 보드게임이 수두룩합니다. 그만큼 보드게임의 원리, 해법, 필승법 등을 수학적으로 분석한 연구도 많죠. 이번 달에는 2017~2018년 수학동아에 연재했던 '보드게임 페스타'에 소개했던 보드게임 일부와 이와 관련된 수학 문제를 소개합니다. 신기한 보드게임도 맛보고 문제도 열심히 풀어보세요!
<1> 달콤한 게임, 촘프
[게임 설명]
①
격자 모양 사각형 초콜릿을 준비하고 왼쪽 맨 아래 조각을 독이 든 조각으로 정한다.
(초콜릿 대신 없으면 모양이 비슷한 블록이나 바둑돌로 해도 좋다.)
②
상대와 번갈아 가며 초콜릿 조각을 선택한 뒤, 선택한 조각을 포함해 오른쪽과 위에 있는 모든 초콜릿 조각, 그리고 이 초콜릿으로 둘러싸인 영역에 있는 초콜릿을 모두 먹는다.
③
이렇게 상대와 번갈아 가며 초콜릿을 먹다가 독이 든 초콜릿 조각을 먹는 사람이 진다.
[게임 예시]
가로 4조각, 가로 5조각인 초콜릿으로 하는 촘프 게임.
[문제]
난이도 ★☆☆
2×3, 2×4, 2×5 촘프에서 처음 선택하는 사람이 이기려면 어떤 조각을 선택해야 할까? 답을 찾았으면 2, 3, 4, 5…. 등 가로의 길이에 상관없이 이길 수 있는 방법을 찾아보자.
---------------------
<2> 내 자리는 어디에? 15 퍼즐
[게임 규칙]
①
액자처럼 생긴 정사각형 틀 안에 1부터 15까지의 숫자가 적힌 사각형 타일이 나란히 놓여있다. 가로세로 4개씩 총 16개 타일이 들어갈 수 있지만, 1칸을 비워 다른 타일을 빈칸으로 움직일 수 있도록 했다.
②
무작위로 배열된 타일을 옮겨 타일에 적힌 숫자를 오름차순으로 배열하면 게임이 끝난다.
이때 숫자가 순서대로 배열된 상태를 ‘표준 배열’이라고 한다.
[게임 예시]
아래 가운데 그림을 보면 6, 7, 10, 11, 12번 타일을 옮겨야 표준 배열을 만들 수 있다. 이 경우 10번 타일을 먼저 아래로 옮긴 뒤 6번 타일을 10번 타일이 있던 자리로 옮기고, 이어서 7번, 11번, 12번 타일을 각각 6번, 7번, 11번 자리로 옮기면 표준 배열을 만들 수 있다.
[문제]
난이도 ★★☆
아래 배열은 가로, 세로, 대각선에 있는 숫자의 합이 30인 마방진임을 확인하고, 표준 배열로 만들 수 있는지 확인해보자. 또, 이 배열에서 14와 15만 서로 바꾸어 새로 배열을 만들었을 경우 표준 배열로 만들 수 있는지도 확인해보자. 표준 배열로 만들 수 있다면 실제로 표준 배열을 찾아보자.
---------------------
<3> 1258 게임
[설명]
①
1, 2, 5, 8로 이뤄진 두 자리 숫자가 적힌 카드를 이용해 십의 자리와 일의 자리 모두에서 1, 2, 5, 8이 한 번씩 나오는 카드 4장을 빨리 찾는 게임.
②
1258카드는 숫자 카드 96장과 어떤 숫자도 되는 조커 2장으로 이뤄져 있다.
1, 2, 5, 8로 이뤄진 두 자리 숫자 카드 16장이 서로 다른 6색으로 칠해져 있어 총 96(=16 ×6)장이다. 또 어떤 카드를 골라도 180° 돌리거나 뒤로 뒤집어서 다른 숫자로 바꿀 수 있다. 예를 들어 15는 51, 12, 21로 변신이 가능하다.
③
가진 카드가 4장 이상일 때 카드를 돌리거나 뒤집어서 십의 자리와 일의 자리에 1, 2, 5, 8이 각각 한 번씩 나오는 4장의 카드가 있으면 이 카드들을 ‘올라 카드’라고 한다.

[문제]
난이도 ★★★
96장의 1258카드 중에 12장의 1258 카드(1세트)를 무작위로 펼쳐 놓았다고 가정하자. 그러면 총 96C12개의 세트 조합이 가능하다. 갯수가 너무 많으니 숫자 1, 2, 5, 8을 치환하거나 카드의 6가지 색을 치환해서 얻어지는 새로운 12장의 1258 카드 세트를 생각하자.
이 변형된 카드 세트는 원래 카드 세트가 갖고 있는 근본적인 성질들을 그대로 갖고 있다. 예를 들어 4장의 올라 세트는 이 변환들에 의해 그대로 보존된다. 따라서 이런 카드 세트는 주어진 카드 세트와 '동등'하다고 한다.
그러면 12장의 1258 카드 세트 중 서로 동등하지 않은 것은 총 몇 가지일까?
-끝-
※알립니다※
12월 23일(월), 서강대학교에서
김종락 교수와 함께 보드게임을 즐기고 관련 문제를 풀어보는 강연을 개최합니다.
자세한 사항은 아래 링크를 참고하세요!
http://www.polymath.co.kr/aboutMath/4392
-
-
-
-
-
용어 설명이 부족했네요! '치환'이란 수학 개념에 대해 아래에 설명을 달아두겠습니다~.
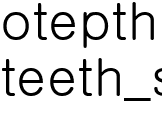
('치환'에 관한 일반적인 설명이 아닌, 이 문제에만 해당하는 설명임을 명심하세요!)
치환 숫자 일부의 위치를 서로 바꾸는 행위.
예시① 1, 2, 5, 8 중 1과 2의 순서를 바꾸는 행위.
예시② 1, 2, 5, 8 중 1과 3의 순서를 바꾸고, 2와 4의 순서를 바꾸는 행위.
세 장의 카드 [12] [25] [18]에 ①을 적용하면? [21] [15] [28]
세 장의 카드 [12] [25] [18]에 ②를 적용하면? [34] [45] [38]
좋아요0 -
감사합니다.
좋아요0 -
3이랑 4는 왜 등장한거죠? 1,2,5,8 이외의 다른 숫자를 써도 되는건가요?
좋아요0 -
3,4는 예시로 들은 것으로 문제를 풀때는 1,2,5,8만 쓰세요.
좋아요0
-
-
-
확인요청중
2열인 경우에는
O O
독O O
과 같이 만들어야 합니다.
그래서 우상단의 한개를 없애야합니다.
그러면 상대가 윗줄을 n개 없애면 저도 아랫줄에 n개 없애면 됩니다.
반대로 상대가 아랫줄에서 n개를 없애면 윗줄에서n개를 없애면 됩니다.
상대가 상대가 다시 직사각형모양이 되도록 잘랐다면 나는 다시 우상단의 한개를 없애면 됩니다.
-
만약 1 x 2라면
초콜릿을 ㅊ이라고 하고 독을 ㄷ이라고 하면
ㅊ
ㄷ 이 되는데 이러면 당연히 저 ㅊ를 먹어야 합니다.(ㅊ이 하나밖에 없으므로 자명함)
2x2라면
ㅊㅊ
ㄷㅊ 인데 이러면 오른쪽 상단의 한개를 먹으면 이깁니다.(그러면 상대가 ㅊ을 한번에 다 없앨 수 없으므로 ㅊ을 하나만 없애게 되고 그러면 당연히 내가 남은 걸 없애므로 이긴다.)
만약 3x2라면
ㅊㅊㅊ
ㄷㅊㅊ인데 이러면 이것도 우측 상단을 먹어야 합니다. 이유는 휠릭시스 님이 아십니다.
만약 4x2라면
ㅊㅊㅊㅊ
ㄷㅊㅊㅊ 인데 이러면 우측 상단을 없애면 휠릭시스 님께서 내린 결론과 같은 이유에서 항상 이기고
5x2라고
ㅊㅊㅊㅊㅊ
ㄷㅊㅊㅊㅊ 인데 이래도 우측 상단을 먹으면 무조건 이기므로
우측 상단걸 먹으면 이기는군요!(이제야 문제를 이해했습니다.)
-
다들 1번은 풀었으므로 저도 공댓을 올리겠습니다. 위에 정답확인요청을 해서 캡처해서 올립니다.


-
그럼 지금까지 봤을 때 1번은 우측 상단 거를 먹으면 된다로 결론이 난 건가요?
좋아요0 -
네.
좋아요0 -
1번은 2019 정보올림피아드 기출문제였습니다. 직접 AI와 게임을 해서 이겨야 했죠.
좋아요0 -
정확하게 맞췄습니다~!
한 문제가 더 풀리면 위 정답 요청한 댓글을 부분해결로 처리할게요!
좋아요0 -
2,3번은 채점 안 해주나요?
좋아요0 -
촘프 게임 문제를 풀어보며 생각해 본 내용을 공유 하고자 합니다.
2×n의 경우에는 언제나 맨 위 오른쪽의 한 칸을 가져가면 되지만, 3×n의 경우에는 3×3이나 3×4에서 2×2를 가져가야 이길 수 있다는 결과가 나옵니다. 하지만 3×5에서는 다시 맨 위 오른쪽 한 칸을 가져가야 하므로 일정한 규칙을 찾기가 힘듭니다. 하지만 언제나 첫 사람이 이길 수는 있습니다.
귀류법을 써서, n×m이 첫 번째 사람이 이길 수 없는 경우라고 가정하겠습니다. 이때 1×1은 제외하겠습니다. 그러면 모든 초콜릿의 상태를 이길 수 있는 경우와 어떻게 해도 지는 경우로 나눌 수 있는데, n×m이 지는 경우이므로 n×m에서 오른쪽 위 한 칸을 제외한 상태는 이기는 경우입니다. 그러므로 두 번째 사람이 그 상태에서 몇 칸을 제외하여 지는 경우로 만들 수 있는데, 그 제외하는 것을 어디에서 뺐든 맨 위 오른쪽 한 칸을 포함한 모양도 함께 뺄 수 있습니다. 그러므로 n×m에서 몇 칸을 빼어 지는 모양이 존재하여 처음 가정이 모순이 되고, 언제나 첫 사람이 이길 수 있습니다.
하지만 아직 이기는 필승전략을 찾지 못했습니다. 저는 이렇게 n×m에 대한 일반화된 필승전략을 찾아보고자 합니다.
좋아요0 -
n*m에 대한 일반화는 불가능합니다.
NYPC 2020 기출 문제여서 깊게 고민해보았고, 일정한 패턴이 등장하지 않음을 알 수 있었습니다.
다만, 점화식으로의 표현은 가능합니다.
좋아요0
-
-
-
확인요청중
2번.
정렬이 되어있지 않은 경우는 어느 숫자 뒤에 나오는 숫자가 더 작은 경우로
각각의 숫자 n에 뒤에 나오는 숫자가 더 작은 경우의수 f(n)을 정의한다.
S=f(1)+f(2)........f(16) 이라 하자.
빈칸이 좌우로 움직이는 경우)
빈칸을 제외하게 된다면, 배열은 같다.
따라서 영향없음.
빈칸이 상하로 움직이는 경우)
빈 칸과 빈 칸과 바꾸는 숫자 사이의 숫자를 생각하자.
총 3개가 존재하며 이들은 빈 칸과 바꾸는 숫자보다 크거나 작다.
그런데 빈 칸과 바꾸는 숫자가 상하로 움직인다는 것은, 이들을 기준으로 앞으로 가거나 뒤로 가게 된다는 말이다.
따라서 +든 -든 사이의 세 숫자는 f(n)이 1씩 변경되게 된다.
+++, ---, ++-, --+ 이렇게 4가지 경우가 나오며,
반드시 S는 1 또는 3만큼의 크기로 바뀌게 된다.
여기서, 고려하지 않은점이 하나있다.
빈 칸은 올라가는 시행과 내려가는 시행의 횟수가 같아야한다.
윗 줄부터 1 2 3 4를 각각부여해 S에 더한다.
이렇게 되면 S는 항상 짝수의 값을 유지한다.
돌아가서, 15와 14가 바뀌어 있는 상태를 보자.
1 2 3 4
5 6 7 8
9 10 11 12
13 15 14 0 (0은 빈 칸이다.)
S = 1이다. 따라서 이 경우 불가능하다.
주어진 배열의 S를 구해보면
위에서 부터, 14+0+0+9+1+6+5+3+3+2+1+1+0+0= 48 이다.
짝수임으로 가능하다.
-
'예를 들어 4장의 올라 세트는 이 변환들에 의해 그대로 보존된다'
이게 대체 무슨말인지 잘 모르겠습니다.
-
-
-
확인요청중
3번 풀이입니다. 동등하지 않다는 것은 숫자의 조합이 다르다는 것입니다. 따라서 숫자의 조합을 세면 됩니다.
1은 12장의 카드에서 최대 18번 나올 수 있습니다. (색이 6개이므로 11 6개와 1이 한 개인 카드 6장) 8도 1과 같습니다.
2와 5는 뒤집으면 같아지므로 같습니다. 따라서 최대 24번 나올 수 있습니다.
이제 문제를 1 18개, 2 24개, 8 18개중 24개를 뽑아 만들 수 있는 조합의 수를 구하여라로 변형이 됩니다.
이 문제는 2가 1개 일때부터 24개 일때까지의 조합의 수를 각각 구해서 더하면 됩니다. 그러면 정답은 14+15+...+18+19+18+17+...+2+1
=270가지 입니다.-
동등하지 않다는 것은 올라세트 인 것이 변환에 의해 올라세트가 아닌 것이 되거나 올라세트가 아닌 것이 올라세트가 되는 것 아닌가요?
제가 이해한 바로는 다음과 같은 접근이 가능합니다.
- 몇가지 중요한 특성들
'1, 8' - > 뒤집어도 여전히 수에 변화 없음, 따라서 이 수가 하나라면 올라세트 절대 불가.
'2, 5' - > 뒤집으면 서로의 수로 바뀜, 따라서 두 수를 합한것이 4이상이면 올라세트일 가능성 존재.
올라세트인 것 -> 올라세트 아닌 것 갯수 = 올라세트 아닌 것 -> 올라세트인 것, 따라서 하나만 구하면 됨(올라세트 아닌 것 -> 올라세트 인 것 으로 구하겠음).
-개요
1) 1, 5, 2 의 수만 존재하거나, 2, 8, 5 의 수만 존재하는 경우
5 나 2를 8 또는 1로 바꾸고, 2 또는 5를 뒤집어 없는 수로 바꾸면 올라세트 가능, 단 항상 만족하지는 않음(특정 조건 존재)
2) 1 또는 8이 하나 존재 하는 경우
1 이나 8을 2 나 5로 바꾼 후 뒤집어서 한 장의 숫자를 보충. 단 항상 만족하진 않음(특정조건 존재)
3) 그외 4종류의 숫자 전부 존재하는 경우
놀랍게도 52와 같은 숫자는 뒤집어도 같기 때문에 이 특성을 활용하여 올라세트가 아닌경우에서 올라세트인 경우로 바꾸는 경우가 존재함. 그러나 그 이상의 경우가 있는지는 확인이 안된상태.
-요지
음.. 제 생각에는 서로 같이 위의 경우에따라 조건을 찾아서 문제를 해결하는 방식을 취해야할 것같습니다. 조건이 너무 까다롭기 때문에 많은 사람의 검토는 필수로 보입니다.
이 문제를 풀 수 있는 핵심적인 아이디어가 더 필요할 지도 모르겠다는 생각을 합니다. 많은 사람이 고민할수록 더 쉽게 풀릴 듯해서 올립니다,
좋아요0
-