폴리매스

참고로 아직 답 구하고 있습니다

아마도 답 구하는데 2일정도 걸릴것 같습니다

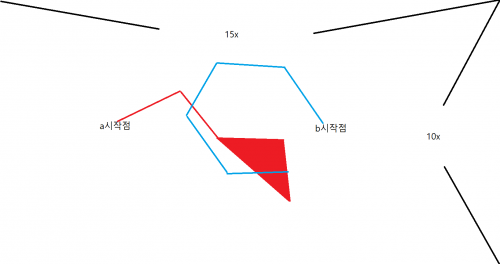
15x * 10x 모양의 영역전쟁판이 있다

(3x,5x)에 A팀(마리나 비아조프스카, 허준이, 아나 카라이아니, 위고 뒤미닐-코팽, 알렉산드로 로구노프)의 시작점이 있고, 

(12x,5x)에 B팀(쑨 쏭, 바르가브 바트, 버리우 페테르, 아이반 코윈, 제이콥 치머만)의 시작점이 있다.

두 팀의 선수들 각각 5번의 '선 긋기' 기회가 있다(팀당 25번).

'선 긋기'란 시작점에서 출발해 길이가 x인 선을 긋는 것이다. 이 선들이 연결되어 면이 되면 그것이 팀의 영역이 되는 것이다. 영역이 겹치면 가장 최근에 그 영역을 얻은 팀이 차지한다.

각 팀 모두 위에 표시된 순서대로 번갈아가면서 선 긋기 기회가 있고, 마지막 선수가 다섯번의 기회를 다 쓰면 경기가 종료된다(풀어 쓰자면 a팀의 마리나 비아조프스카가 1번째 선 긋기를 하고 그 다음에 b팀의 쑨 쏭이 1번째 선긋기를 하고 a팀의 허준이가 1번째 선 긋기를 하고....... a팀의 마리나 비아조프스카가 2번째 선 긋기를 하고 b팀의 쑨 쏭이 2번째 선긋기를 하고...... b팀의 제이콥 치머만이 5번째 선긋기를 하면 게임이 끝난다).

양 팀의 선수들은 모두 똑똑한 수학자이므로 최선의 전략을 쓸 것이다.

그런데 각 팀에는 1명의 스파이가 숨어있다. 스파이는 5번의 선긋기 중 1번 '배신' 기능을 쓸 수 있다. 배신 기능은 원래 있었던 전략에서 벗어나 자기 맘대로 팀의 전략을 방해해 영역을 좁게 하거나 망가뜨릴 수 있다. 

1) 양 팀이 시전할 최선의 전략은 무엇인가? 참고로 a팀이 선공, b팀이 후공이다. (이 부분에서는 제가 틀렸을 수도 있으므로 제 풀이보다 더 좋은것이라면 그것을 답으로 지정하겠습니다). 

2) 스파이들은 자신의 몇번째 차례에 '배신' 기능을 사용하는 것이 가장 효율적일까?