함께 풀고 싶은 문제
창의력을 기를 수 있는 수학 문제 또는 퍼즐을 내는 곳입니다.
[창의 퍼즐] 관리자에 의해 삭제된 개시글입니다.
NINE-FOUR=FIVE
이 복면산의 해를 모두 구하라(단문이면 삭제합니다.)
이 문제 어떠셨나요?
좋아요
1
글쎄요
0
어려워요
0
댓글 8
댓글 작성하기
-
관리자에 의해 삭제된 것이 아닌 이유
1. 개시글 철자 오류
2. 삭제됬으면 친절하게 삭제되었다고 제목이 되진 않는다
3. 함풀문 페이지에 뜬다
-
해결
-
다시 도전
'이따' 풀이 올리겠다고 한지 벌써 이틀이네요... 그러면 풀이 써보겠습니다. 다른 문자는 다른 숫자를 뜻한다고 생각하고 풀었습니다.
풀이) 먼저 R=0인 것은 자명하다. 다음으로 O의 값을 생각해보자. O의 값은 0은 될 수 없다. 그런데, 100의 자리가 I인 수에서 100의 자리가 O인 수를 빼었음에도 불구하고 100의 자리가 그대로 I인 경우는 백의 자리에서 받아내림이 발생하고 O=9인 경우일 수밖에 없다.
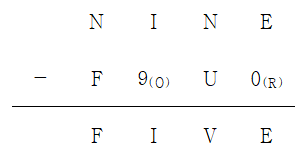
따라서, (10+N)-U=V이고, (N-1)-F=F이다. 즉 U+V=N+10이고, N=2F+1이다. N은 홀수이고 O의 값이 이미 9이므로 N으로 가능한 수는 1, 3, 5, 7이다.
(i) N=1: F=0=R이므로 겹친다. (X)
(ii) N=3: F=1이고 U+V=13이므로 (U, V)=(5, 8), (6, 7), (7, 6), (8, 5). I는 겹치지 않는 수 아무거나 해가 된다.
(iii) N=5: F=2이고 U+V=15이므로 (U, V)=(7, 8), (8, 7). I는 겹치지 않는 수 아무거나 해가 된다.
(iv) N=7: U+V=17이어야 하는데 U, V 중 9가 있어서는 안 되므로 불가능하다. (X)
-
부분해결
-
닫기
