
임의의 위치에 직선 5개가 있다.
그 직선은 모두 적어도 다른 1개의 직선과 닿아있다.
모든 직선의 각도는 무작위다.
그럼, 그 직선 5개가 5각형을 이룰 확률은?
좋아요
0
글쎄요
0
어려워요
0
-
해결
무논리와 노가다로 점철된 풀이입니다..ㅎ
오각형의 성질에 의해 오각형의 내각의 합은 540' 입니다
임의의 오각형에 대해 인접한 변들끼리 이루는 각을 차례대로 a, b, c, d, e 라고 했을때
이 각각의 각은 (0, 180) 범위내에 존재해야합니다
따라서 a + b + c + d 의 값은 (360, 540) 범위내에 들어가야 한다고 생각했습니다
그리고 이때 역시 각각의 각 a, b, c, d 또한 (0, 180) 내에 존재하고
실수분포는 연속균등분포 따른다고 보고
문제에서 구하는 값은 연속균등분포의 합에서 나올수 있는 값의 범위로 생각했습니다
사실 이에 대한 자세한 과정은 배우지 않아 일단 코딩으로 풀었습니다
```c++
#include <bits/stdc++.h>
#define MAX 10000000
using namespace std;
int main(){
mt19937 mt(time(nullptr));
uniform_real_distribution<double> dist(0, 180);
auto gen = bind(dist, mt);
long hit = 0;
for (int t = 0 ; t < MAX; t++){
double current = 0;
for (int i = 0 ; i < 4; i++){
current += gen();
}
if (360.0 < current && current < 540.0) hit++;
}
cout << (double)((double)hit / MAX);
}
```
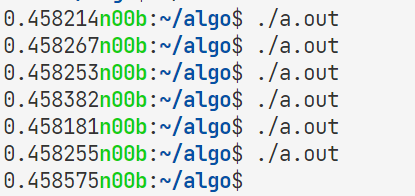
대략적인 확률은 45.8정도로 나옵니다
후에 찾아보니 Irwin–Hall_distribution 이라는 것이 확률밀도식이 따로 존재해 적분을 해보았습니다
(참고. Irwin–Hall distribution - Wikipedia)
저희가 구하려는 값을 정규화해서 적분을 하면
약 45.833 이 나옵니다











