폴리매스

문제 시작에 앞서

이 문제는 저의 흑역사 시절 만들어진 문제입니다.

그러니 그 이야기는 지금은 하지 말아주세요!

또, 원작은 세바문이였으나 이 문제는 창퍼로 내겠습니다.

끌올로 세바문가는건 좀 그런 것 같아서요 ^ㅡ^

재미있게 풀어주세요!

(원작에서 댓글도 하나 안 달렸다는...)

수파는 학교에서 리코더 수업을 들었는데, 오늘은 시험 날이었다. 다행이 여러분이 생각하는 모의고사 아니어서 공부 하나도 않...웁웁

다 맞는지 확인을 했는데 해설만 길었다. 그래서 수파는 남는 여백에다 낙서를 했다. 시험지를 제출하지 않으니 별로 낙서에 큰 문제는 없...((퍽퍽

근데 그러다 우연히 수학문제를 발견했다.

수파는 이것을 매트로그램(matrogram) 이라 이름붙였다.

매트로그램이란, n*n격자에 각 구멍 테두리에 꼭짓점 부분의 사각형은 2개, 꼭짓점을 제외한 테두리 부분의 사각형은 3개, 다른 곳은 4개에 화살표를 그린다.

(3*3격자 매트로그램에 예시)

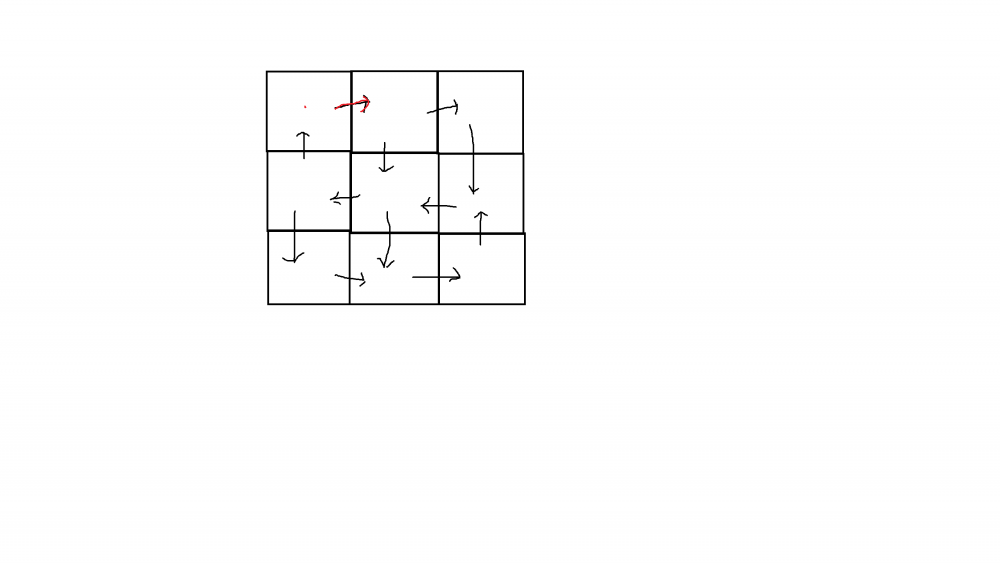
그런 다음, 저 그림에 있는 빨간 점에서부터 움직인다.

움직일 때에는 그려져있는 화살표대로만 가야 한다.

단, 위에 그림에서 나온 것 처럼 처음 움직일 때에는 저 빨간색 화살표로 가야 한다.

그리고 매트로그램에 어떤 모양은 움직이기가 불가능해진다.

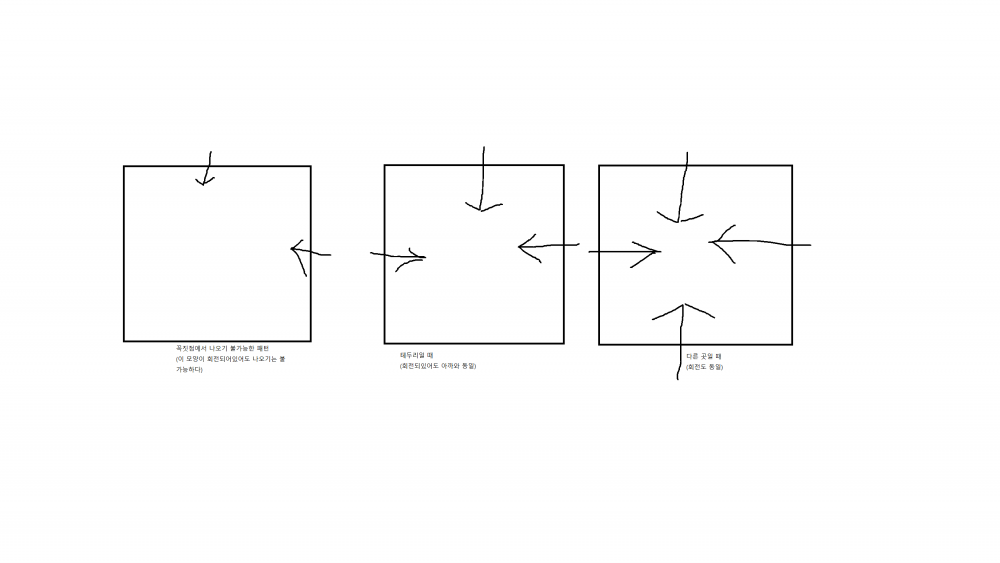
이 세가지 패턴이다.

그럼 이 예를 살펴보자.

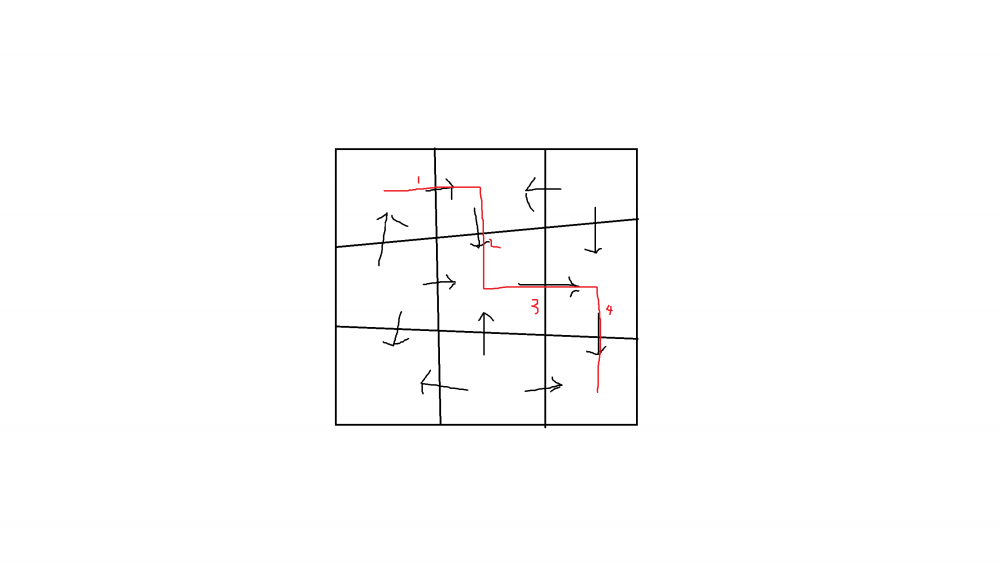
이 그림은 모든 격자를 다 돌기 불가능한 매트로그램이다.

그럼 이 그림의 선은 격자와 격자 사이에 선을 모두 4번지났으니

이건 노선의 길이가 4인 매트로그램이 된다. 앞으로는 짧게 표기하기 위해 노선의 길이가 n이면 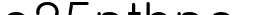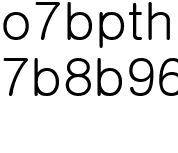이라 하고, 격자는 격자가 n*n이면 으로 표기하도록 하겠다.

문제

(1) 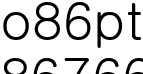일 때 모든 격자의 경계를 지나는 모양(노선이 2*2격자 모양을 만들 때)을 만드는 매트로그램은 모두 몇 가지인가?

(2) 일 때는 모든 격자의 경계를 지나는 매트로그램은 모두 몇 가지일까?

(3) 일 때 모든 격자의 경계를 지나는 매트로그램의 수를 n을 이용하여 나타낼 수 있을까?

-1,2번 풀면 해결

-3번풀면 추가해결