함께 풀고 싶은 문제
깊이 고민해볼 수 있는 수학 문제를 내는 곳입니다
[세상을 바꿀 문제] 함성프(함께 성장하기 프로젝트)-4차원
數弦님의 함성프 많이 참여해 주세요.
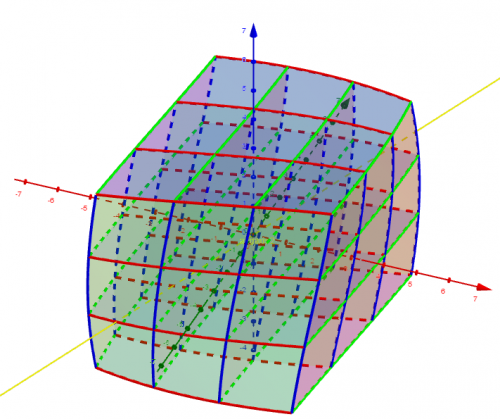
문제:4차원 테서랙트의 넓이는 어떻게 구하는 것이 좋을까요?
정답요청은 공개댓글로 해 주시고 참신한 의견에는 해결딱지를 드리겠습니다.
이 문제 어떠셨나요?
좋아요
0
글쎄요
0
어려워요
0
댓글 6
댓글 작성하기
-
해결
수학에서 차원이란, 점을 확정시키기 위한 변량의 개수, 움직일 수 있는 벡터의 개수입니다.
4차원 직육면체는 변량의 개수가 4개며, 모두 수직이니
이 변량들의 양을 4개, 즉 모두 곱하면 될 것 같네요.
-
1. 직육면체는 4차원에 존재할 수 없습니다. (z축이 존재하지 않는 정사각형이 3차원에 없는 것과 같은 문제)
2. 직육면체는 넓이를 구할 수 없습니다.
-
다시 도전
-
차원의 정의는 주어진 공간에 있는 점의 위치를 표현하기 위해 필요한 숫자의 개수입니다
위치를 어떤 방향으로도 표현할수 없는 점이 0차원,
1방향(직선)으로 표현할수있는 선이 1차원(선의 길이)
2방향(가로,세로)으로 표현할수있는 면이 2차원(가로x세로로 넓이 계산)
3방향(가로,세로,높이)으로 표현할수있는 입체가 3차원(가로x세로x높이로 넓이 계산)
그럼 4차원 테서렉트(4차원 큐브입니다 뫼비우스님은 이걸 말하고 싶었는데 단어를 몰라 4차원 직육면체라 한 것이겠죠) 4방향으로 표현이 가능하니(가로x세로x높이x다른 방향으로 계산이 가능하겠네요
닫기
