1. 단순문제를 왜 내면 안 되는지에 관하여 여러분 대다수가 알고 계시다고 생각합니다(아직 모르시는 몇몇 분들도 계시지만요. 다른 분들이 알려주시리라 믿습니다). 가볍게만 설명하면, 내면 안되는 이유는 다음과 같습니다.
1) 매스펀은 레벨을 올리는 목적으로 활용되어서는 안 된다.
2) 단순문제는 만드는 데 의미가 없으며 푸는 데 재미도 없다.
3) 단순문제를 다수 출제 시 다른 문제들을 푸는 데 방해될 수 있다.
2. 그러나 단순문제가 '무엇인지'에 관하여 여러분 다수가 오인하는 부분이 있는 것으로 보입니다. 어떻게 아냐고요? 매스펀에 들어가보면 단순문제로 보기 어려운 문제도 글쎄요가 2~3개씩 올라가 있거든요.
1) 쉽다고 단순문제가 아닙니다.
2) 짧다고 단순문제가 아닙니다.
3) 기본 개념을 활용하여 푼다고 단순문제가 아닙니다.
4) 한번에 많이 낸다고 단순문제가 아닙니다.
단순문제는 생각의 여지를 주지 않는 문제입니다. 예를 들어, 1+1은 단순문제입니다. 이는 쉬워서도, 짧아서도, 기초적인 개념이라서도 아닙니다. 누구나 1+1=2임을 알고 있고 또 누구나 출제할 수 있는 문제이기 때문입니다. 더 정확히 얘기하면, 생각 없이 낼 수 있는 문제이기 때문입니다.
그러나 다음 문제를 봅시다.
1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+1=?
(예시가 더하기다 보니 비슷한 수준의 어려운 문제를 내기는 힘들었습니다. 그러나 중등 수학 이상의 개념을 활용하면 의미를 이해하지 못하는 분이 계실 거라 생각하여 예시는 초등학교 수학 이하의 수준을 활용해 낼 것입니다.)
위의 문제는 단순문제일까요?
정답은 '그럴 수도 있고, 아닐 수도 있다' 입니다.
'??? 이게 왜 단순문제가 아님???'라고 생각하셨다면 정상입니다. 하지만 생각해봅시다.
생각의 여지를 주지 않습니까? 아니요. 생각의 여지는 존재할 것 같은데요. 분명 노가다로 세는 방법을 제시한다면 답답한 쓰레기 문제겠지만, 저희는 (제 기억과 현재 초등학교 교육과정이 차이가 나지 않는다면) 초등학교 5학년에 '어림'을 배웁니다. 위 문제는 4줄로 되어있고 한 라인에 약 50개의 1이 있다고 가정하면 대충 답이 200이 됩니다.(실제 답은 228입니다. 혹시 세어보는 사람이 있을까봐 미리 말해줬어요!)
예시가 이런거라서 그렇지, 다른 예시도 충분히 많습니다. 다른 예를 하나 봅시다.
'2 - 5 - 8 - 13 - 16 - 21 - 26 - 31 - 34 - ?'
답은 39입니다. 왜냐고요? '소수일때는 3을 더하고 소수가 아닐때는 5를 더한다'라는 룰이거든요.
이런 암호/규칙/수열 문제는 (보통은) 단순문제의 끝판왕입니다. 하지만 봅시다. 쉽습니까? 우리 지상 최대의 천재들만 모여있는 수학동아-폴리매스 이용자들이라면 당연히 풀 수 있는 문제이지만 대다수의 사람은 이 문제를 풀지 못할 겁니다99%의 사람들이 이 문제를 풀지 못합니다!
아니면, 짧습니까?

기본 개념입니까? 이는 무려 중학교 1학년 때 배우는 '소수와 합성수', 고등학교 2학년때 배우는 '수열'을 섞어놓은 세계적인 난제 반열의 문제입니다!!(구라입니다.)
이 문제를 단순문제로 보아야 하는 이유는 두가지입니다.
첫째, 문제에 성의가 없습니다. 조금 아까의 판단 기준으로 한번 더 봅시다. 과연 '이 문제를 저만 낼 수 있습니까?'


대부분의 수열 문제는 정성들여 만들지 않습니다. 왜냐고요? 그냥 모든 계수가 정수인 다항함수식 하나 생각한 다음에 1, 2, 3, ... 넣으면 되거든요.
그리고 대부분의 이런 식의 수열 문제는 답이 하나로 정해지지 않습니다. 예시의 수보다 최고차항의 지수가 크기만 하면 이런 다항함수는 몇개든 만들 수 있거든요!
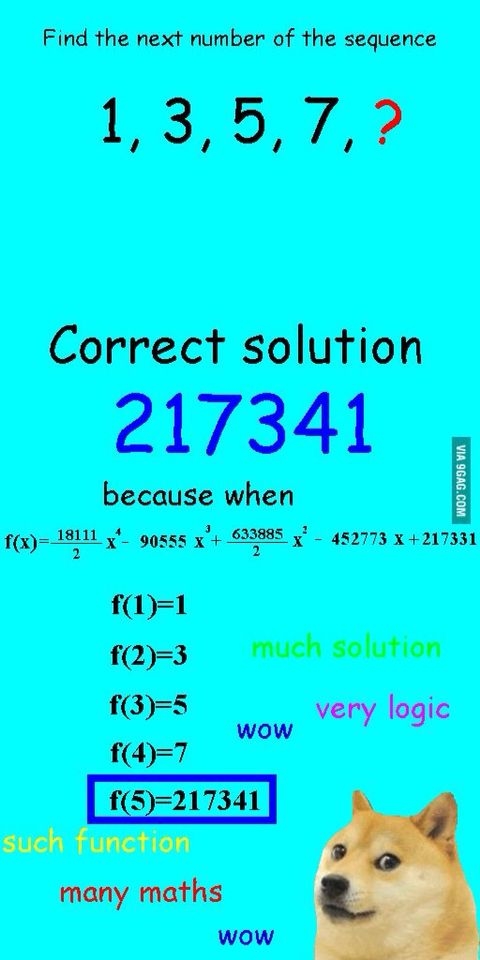
물론 수열 문제도 정말 여러 규칙을 고려하며 고심 끝에 결정한 하나의 규칙을 문제로 냈을 수도 있습니다. 그럴 때는 두번째 조건을 봅시다!
둘째, 문제가 확장되지 않습니다. 쉽게 말해서, 재미없게 문제를 낸다는 말입니다. 예를 하나 들어봅시다.
다음을 풀어라: dksl dlrj dho gksrmffh dksqkRnla ;; dksl slaemfdk dlrj gksdudzlrk wkrehddl dksehldy;;
이 문제를 풀 수야 있겠죠. 그러나 풀고 싶습니까? 아무도 제 한영키의 작동 여부에 대해 궁금해하지 않습니다.
여기서 저희는 함풀문의 존재 이유를 물어볼 필요가 있습니다. 이 부분은 아인수타인 님의 글 일부분을 발췌하겠습니다.

(원본: http://www.polymath.co.kr/contents/view/28534?page=1 아직 읽지 않으셨다면 제 글을 다 읽고 이 글도 꼭 읽어보세요)
과연 수열 문제, 암호 문제, 단순 계산 문제 등이 '펀'할지, 함께 풀고 싶어 낸 문제인지를 생각해 봅시다.
이는 주관적인 내용이지만, 동시에 '사회적인' 내용이라고 생각됩니다. 즉, 대부분의 사람이 이 출제 의도에 관하여 어느 정도 파악할 수 있다는 뜻입니다!
또 예시 하나 봅시다.

분명 쉬운 문제는 맞습니다. 그러나 다양한 방법을 생각해 볼 수 있고 재미있게 풀 수 있는 문제입니다! 충분히 다른 사람들과 함께 풀고 싶어 낸 문제라는 것이 와닿지 않습니까?
제가 확장 가능한 문제, 즉 열린 문제라고 말했지만, 꼭 그런 것도 아닙니다. 충분히 즐길 수 있는 문제인지를 생각해 보시면 판단하기 더 수월해질 겁니다.

오늘은 단순 문제와 보통 문제를 구분하는 방법에 대해 배워보았어요~
저는 개학하고 나서 폴리매스에 돌아오도록 하겠습니다!














