폴리매스

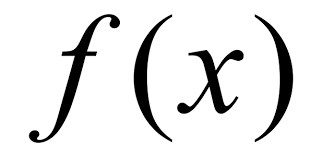
[f(x)+f(y)=f(x+y) 함수방정식에 대한 연구]

f(x)+f(y)=f(x+y) 꼴의 함수방정식은 일명 '코시함수방정식'이라고 불리며, 많은 성질들을 가지고 있다.

=======================================================================================================

1) f:R=>R, f(x)+f(y)=f(x+y)의 해는 f(x)=cx (단, c는 상수) 밖에 없는가? 그렇다면 그것을 증명하고 아니라면 그 이유를 말하라.

2) f(x)+f(y)=f(x+y) (단,x는 모든 실수, y는 y>=0인 모든 실수)이라는 식이 성립할 때, f(x)+f(y)=f(x+y) (단, x,y는 모든 실수)가 성립함을 보여라.

3)f:R=>R, f(x)+f(y)=f(x+y)이 성립하고 f(x)는 연속함수 일때 f(x)=cx(단, c는 상수)임을 보여라.

4)f:R=>R, f(x)+f(y)=f(x+y)이 성립하고 f(x)는 특정 구간에서 유계(즉, 어떤 임의의 구간에서 함숫값이 어떤 수 이상이라는 것) 일때 f(x)=cx(단, c는 상수)임을 보여라.

5) f:R=>R, f(x)+f(y)=f(x+y)이 성립하고 f(x^3)=xf(x^2) 일 때 f(x)=cx임을 보여라.

3개 이상 풀면 해결 하나, 5개 다 풀면 해결  두개 드립니다 :)