폴리매스

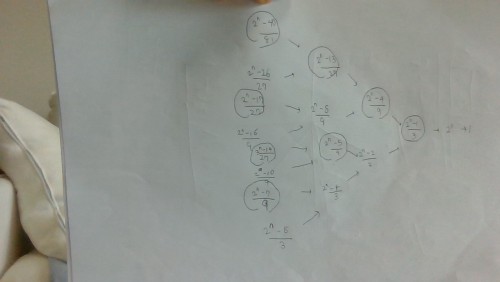
1. 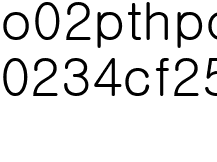일때

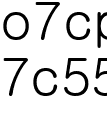이므로 추측을 성립한다.

2. 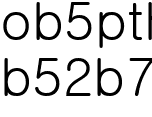일때 (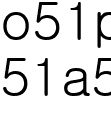은 2가 아닌 소수)

결국은 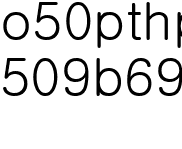가 약분되어 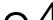가 된다는 겁니다.

3. 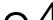 일때

그리고 왜 모든 자연수가 1,2,3 경우중 한 가지인지는 킹갓제너럴엠페러충무공마제스티 켋님이 풀어주셨슴다. (오류 있으면 제보 부탁드립니다..)

1번과 2번 경우의 n은 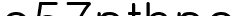이고

3번 경우의 n은 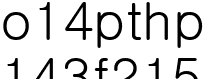 이기 때문에

모든 자연수(1을 제외)가 1,2,3 경우중 한가지가 됩니다.

근데 여기에 사진은 어떻게 올리는 거지... 그냥 대표이미지에 올리면 되는 건가요...? (1달 전에 가입한 유저여서 잘 모름 ㅠㅠ)

걍 대표 이미지에 올리는 게 괜찮을 거 같음..

아 맞다. 여기서 문제 하나 올려야 겠네요

추측이 맞으려면은 일단 마지막이 1이 되야 하잖아요? 

그렇다면 모든 자연수는 규칙에 따라서 하다보면 언젠가는 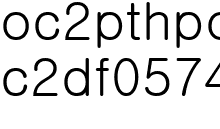이 되어야 하나요?

이게 맞다고 증명해주시면, 대표이미지에 올리겠습니다.

걍 맞다고 가정하고 대표이미지에 올리겠습니다. 

홀수 친 거는 홀수이고요. 어차피 여기서 n은 자연수니까 n+α도 n으로 나타냈습니다. 동그라미를 무한 번 치다 보면 언젠가는 중복되는 게 나오지 않을까요. 그니까 다시 말해서 똑같은 홀수가 나올 수도 있지 않을까요.. 

혹시나 문제 이해 안되면 댓글로 말해주세요. 다시 설명해드릴게요..

<정리>

1. 모든 자연수는 규칙에 따라서 하다보면 언젠가는 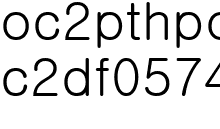이 되어야 하나요?

2. 동그라미를 무한 번 치다 보면 언젠가는 중복되는 게 나오지 않을까요. 그니까 다시 말해서 똑같은 홀수가 나올 수도 있지 않을까요..?