함께 풀고 싶은 문제
창의력을 기를 수 있는 수학 문제 또는 퍼즐을 내는 곳입니다.
[창의 퍼즐] [과학을 위한 수학] 벡터를 알아야지!
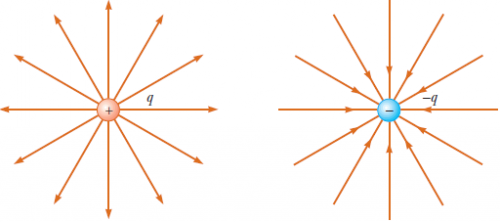
좌표평면의 원점에 점전하가 하나 놓여 있다. 물음에 답하시오.
#1. 이 점전하로 인한 p(x, y)에서의 전기장을 x와 y에 관한 함수로 나타내고 그 과정을 서술하시오. 단, 다음 조건을 준수하시오.
가) 이 좌표평면의 좌표축은 직교좌표계이다.
나) 점전하와 거리가 r 떨어진 점에서 전하량이 Q인 입자가 받는 전기력의 크기는 kqQ/r^2이다. 단, k는 쿨롱 상수, q는 점전하의 전하량이다.
다) 전기장이란 +1쿨롱으로 대전된 test charge가 받는 힘이다.
라) 문제의 최종 정답에서 극좌표를 이용하거나 각도가 변수로 사용되서는 안된다. 단, 과정에서는 이용해도 무방하다.
마) 과정에서 각도를 사용한 경우 단위는 라디안으로 통일하라.
바) 과정의 끝부분에서는 좌표평면 위의 한 점인 Ptest(1, 1)을 활용해 유도한 함수를 검산하여라.
사) 필요한 상수가 문제에서 주어지지 않은 경우, 문자로 놓고 풀어도 좋다.
#2. 점전하의 전하량이 +1쿨롱이라고 하자. 좌표평면 위에서 운동하는 +1쿨롱으로 대전된 입자는 속도와 입자의 질량에 무관하게 좌표평면의 원점을 지날 수 없음을 보여라.
이 문제 어떠셨나요?
좋아요
0
글쎄요
0
어려워요
0
닫기
