함께 풀고 싶은 문제
깊이 고민해볼 수 있는 수학 문제를 내는 곳입니다
[세상을 바꿀 문제] [도형][무한과 유한]원자폭탄으로 파리잡기
1. 일칠이는 얼마전부터 자신의 머리 위를 계속 잉잉거리며 돌아다니는 파리가 매우 거슬렸다.
그래서 원자폭탄으로 파리를 잡으려고 한다.
근처 마트에서 산 이 원자폭탄(?)은 불행히도(다행히도) 성능이 불량이라 효과가 원자폭탄의 중심으로부터 반지름이 1m인 원 안 또는 그 원의 둘레 위다.
만약 하늘이 그리드처럼 생겼다면 파리와 원자폭탄이 추격전을 벌일 때,
파리는 1초에 한 번씩 전후좌우대각선으로 움직일 수 있고(위아래는 안 된다), 원자폭탄은 전후좌우대각선 중 한 방향으로 2초에 한 번씩 2칸씩 움직인다.
또 원자폭탄이 파리를 잡을 수 있는 경우가 생기면 원자폭탄은 그 자리에서 폭탄을 쏘고, 그 폭탄은 원자폭탄이 그리는 원의 중심에 떨어지며, 그 폭탄이 떨어지는데는 1초가 걸린다.
그리고 파리는 자신이 움직이는 것을 이용해 원자폭탄이 떨어질 때에도 전과 같은 규칙으로 움직일 수 있다.
만약 원자폭탄이 파리에게 정통으로 떨어지면 파리는 사망한다. 그러나 원자폭탄의 범위가 미치지 않는 곳에 파리가 있다면 제한구역은 원자폭탄이 떨어진 점에만 생기고, 파리가 그 점에 닿으면 사망한다.
만약 하늘 그리드가 무한하다면 파리가 계속 도망치는 한 원자폭탄에 맞지 않는 것을 증명 혹 반증하시오.
2. 위와 같은 규칙에서 하늘 그리드가 유한하다면 파리는 살아남을 수 있을까?
풀이 필수, 문제에 오류가 있으면 알려주세요!
이 문제 어떠셨나요?
좋아요
4
글쎄요
0
어려워요
1
댓글 10
댓글 작성하기
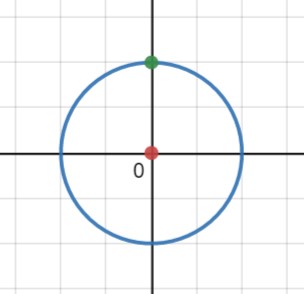와 같고, 초록색은 파리, 빨간색은 원자폭탄입니다.
닫기
