함께 풀고 싶은 문제
창의력을 기를 수 있는 수학 문제 또는 퍼즐을 내는 곳입니다.
이 문제는 오늘 오후 6시에 삭제됩니다. 로딩 시간이 오래 걸리는 경우 등에만 이 곳에 올려주세요.
모든 양의 정수 
에 대하여, 변의 길이가 각각 
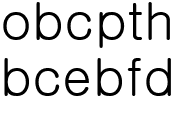인 직사각형이 한 개씩 있다.
무한히 많은 이 직사각형들을 변의 길이가 1인 정사각형 내부에 겹치지 않고 모두 채울 수 있을까?
(참고로 이 직사각형들의 넓이의 합은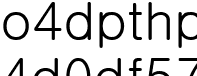 
이다.)
-출처 : Exercise 2.37, Concrete Mathematics (Graham, Knuth, and Patashnik)-
이 문제 어떠셨나요?
좋아요
0
글쎄요
0
어려워요
0
닫기
