우선, kmo를 대비하실 경우 이미 인지하고도 남았을 듯 하다만은,
점화식의 경우 변량이 지정된 특정 값 이상일 경우에 한하여
'특정 단일 원칙'이 성립함을 활용하여 일반화하는 방안임은 아실 듯 하니
조합 파트에서 사용되어지는 부분에 대하여 비중있게 다루도록 하면
네. 조합 내에서는 '특정 단일 원칙'이라 언급한만큼
일단 전체 경우수를 변수값에 상이하게 단일 함수 혹은 수열로 표현,
종속되어지는 경우로 분배하여 식을 수립하는 정도로 활용됩니다.
혹여 장문으로만 설명하면 부분적으로라도 이해가 가시지는 않을 듯도 하기에
기초적인 예에 관하여 언급하면
계단을 1,2개의 계단을 이동함으로서 상부로 이동하는 경우수
를 구하고자 할 경우
위 조건을 충족하는 경우수를 f(n)이라 치환하면
1계단 혹은 2계단을 이동하기에
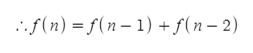
가 성립되어짐이 입증됩니다.
심히 간결하기는 하네요.
근본적인 원리는 앞서 작성한 정도입니다.
그럼 역시나 문제를 해결토록 하여 해당 방안에 대한 감을 상향토록 하죠.

물론 위에 제시한 문제도 별건 없습니다.
지정된 직사각형 내에 개별 직사각형을 배치토록 한 후의 경우의 수를 총합산할 경우
답에 해당하는 값이 산출되어질 터이기에,

위 식이 성립 가능하게 하는 요인에 관하여 고찰하면...
타 부분은 전원 인지하실거라 추측되어지나
2*2 유형의 직사각형을 배치할 경우 2*1형상의 물을
가로로 눕히도록 함으로서 2*1배치에는 미포함토록 하는 경우 및
...
네.
다들 이해하셨을 터이기에 해당 정도로만 언급하고
수열 유형에 관하여도 설명하려는 하나
수열의 경우에도 앞서 제시한 방법과 동일히 활용하면 될 터이기에..
점화식을 활용하여 최종 값을 산출하는 방안은
일반적인 해석 파트에서의 일반화 과정에 비하여는
도출하려는 변수의 값이 상대적으로 하향키에 f(x)의 1부터 4의 값을 대입하였을 시의 값은
노가다로, 이후의 값은 점화식에 대입토록 함으로서 산출하시는 방안이
소요 시간을 상대적으로 소화 가능합니다.
오늘자 조합 강의의 경우도 하단 문제를 해결토록 하시는 것을 추천드리며, 이상 종료토록 하겠습니다.

원본: [폴리매스 카페] https://cafe.naver.com/polymathfun/7096









