A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_URI::$config is deprecated

Filename: core/URI.php

Line Number: 101

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Router::$uri is deprecated

Filename: core/Router.php

Line Number: 127

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$benchmark is deprecated

Filename: core/Controller.php

Line Number: 75

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$hooks is deprecated

Filename: core/Controller.php

Line Number: 75

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$config is deprecated

Filename: core/Controller.php

Line Number: 75

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$log is deprecated

Filename: core/Controller.php

Line Number: 75

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$utf8 is deprecated

Filename: core/Controller.php

Line Number: 75

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$uri is deprecated

Filename: core/Controller.php

Line Number: 75

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$exceptions is deprecated

Filename: core/Controller.php

Line Number: 75

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$router is deprecated

Filename: core/Controller.php

Line Number: 75

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$output is deprecated

Filename: core/Controller.php

Line Number: 75

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$security is deprecated

Filename: core/Controller.php

Line Number: 75

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$input is deprecated

Filename: core/Controller.php

Line Number: 75

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$lang is deprecated

Filename: core/Controller.php

Line Number: 75

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$load is deprecated

Filename: core/Controller.php

Line Number: 78

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Cache::$apc is deprecated

Filename: libraries/Driver.php

Line Number: 188

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Cacher.php
Line: 22
Function: driver

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Cacher.php
Line: 17
Function: initiateCache

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Cache::$file is deprecated

Filename: libraries/Driver.php

Line Number: 188

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Cacher.php
Line: 22
Function: driver

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Cacher.php
Line: 17
Function: initiateCache

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$cache is deprecated

Filename: core/Loader.php

Line Number: 1279

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Cacher.php
Line: 22
Function: driver

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Cacher.php
Line: 17
Function: initiateCache

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$cacher is deprecated

Filename: core/Loader.php

Line Number: 1279

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$jscript is deprecated

Filename: core/Loader.php

Line Number: 1279

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Return type of CI_Session_files_driver::open($save_path, $name) should either be compatible with SessionHandlerInterface::open(string $path, string $name): bool, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice

Filename: drivers/Session_files_driver.php

Line Number: 132

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Return type of CI_Session_files_driver::close() should either be compatible with SessionHandlerInterface::close(): bool, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice

Filename: drivers/Session_files_driver.php

Line Number: 290

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Return type of CI_Session_files_driver::read($session_id) should either be compatible with SessionHandlerInterface::read(string $id): string|false, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice

Filename: drivers/Session_files_driver.php

Line Number: 164

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Return type of CI_Session_files_driver::write($session_id, $session_data) should either be compatible with SessionHandlerInterface::write(string $id, string $data): bool, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice

Filename: drivers/Session_files_driver.php

Line Number: 233

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Return type of CI_Session_files_driver::destroy($session_id) should either be compatible with SessionHandlerInterface::destroy(string $id): bool, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice

Filename: drivers/Session_files_driver.php

Line Number: 313

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Return type of CI_Session_files_driver::gc($maxlifetime) should either be compatible with SessionHandlerInterface::gc(int $max_lifetime): int|false, or the #[\ReturnTypeWillChange] attribute should be used to temporarily suppress the notice

Filename: drivers/Session_files_driver.php

Line Number: 354

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: Warning

Message: ini_set(): Session ini settings cannot be changed after headers have already been sent

Filename: Session/Session.php

Line Number: 284

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: Warning

Message: session_set_cookie_params(): Session cookie parameters cannot be changed after headers have already been sent

Filename: Session/Session.php

Line Number: 291

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: Warning

Message: ini_set(): Session ini settings cannot be changed after headers have already been sent

Filename: Session/Session.php

Line Number: 306

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: Warning

Message: ini_set(): Session ini settings cannot be changed after headers have already been sent

Filename: Session/Session.php

Line Number: 316

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: Warning

Message: ini_set(): Session ini settings cannot be changed after headers have already been sent

Filename: Session/Session.php

Line Number: 317

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: Warning

Message: ini_set(): Session ini settings cannot be changed after headers have already been sent

Filename: Session/Session.php

Line Number: 318

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: Warning

Message: ini_set(): Session ini settings cannot be changed after headers have already been sent

Filename: Session/Session.php

Line Number: 319

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: Warning

Message: ini_set(): Session ini settings cannot be changed after headers have already been sent

Filename: Session/Session.php

Line Number: 377

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: Warning

Message: ini_set(): Session ini settings cannot be changed after headers have already been sent

Filename: drivers/Session_files_driver.php

Line Number: 108

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: Warning

Message: session_set_save_handler(): Session save handler cannot be changed after headers have already been sent

Filename: Session/Session.php

Line Number: 110

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: Warning

Message: session_start(): Session cannot be started after headers have already been sent

Filename: Session/Session.php

Line Number: 143

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$session is deprecated

Filename: core/Loader.php

Line Number: 1279

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$agent is deprecated

Filename: core/Loader.php

Line Number: 1279

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$contentsStatus is deprecated

Filename: libraries/Common.php

Line Number: 64

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 64
Function: _error_handler

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 24
Function: initContentsStatusInfo

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$articleStatus is deprecated

Filename: libraries/Common.php

Line Number: 71

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 71
Function: _error_handler

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 24
Function: initContentsStatusInfo

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$db is deprecated

Filename: core/Loader.php

Line Number: 390

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/models/ver3/Contents_model.php
Line: 15
Function: database

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 440
Function: model

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 29
Function: initMenu

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_DB_mysqli_driver::$failover is deprecated

Filename: database/DB_driver.php

Line Number: 371

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/models/ver3/Contents_model.php
Line: 15
Function: database

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 440
Function: model

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 29
Function: initMenu

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents_model::$best_cnt is deprecated

Filename: ver3/Contents_model.php

Line Number: 17

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/models/ver3/Contents_model.php
Line: 17
Function: _error_handler

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 440
Function: model

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 29
Function: initMenu

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents_model::$popular_cnt is deprecated

Filename: ver3/Contents_model.php

Line Number: 18

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/models/ver3/Contents_model.php
Line: 18
Function: _error_handler

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 440
Function: model

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 29
Function: initMenu

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$member_model is deprecated

Filename: core/Loader.php

Line Number: 353

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/models/ver3/Contents_model.php
Line: 20
Function: model

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 440
Function: model

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 29
Function: initMenu

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$contents_model is deprecated

Filename: core/Loader.php

Line Number: 353

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 440
Function: model

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 29
Function: initMenu

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$menuList is deprecated

Filename: libraries/Common.php

Line Number: 561

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 561
Function: _error_handler

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 29
Function: initMenu

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$common is deprecated

Filename: core/Loader.php

Line Number: 1279

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$dto is deprecated

Filename: core/Loader.php

Line Number: 1279

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 14
Function: __construct

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$together_end_date is deprecated

Filename: ver3/Contents.php

Line Number: 17

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 17
Function: _error_handler

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Cache::$dummy is deprecated

Filename: libraries/Driver.php

Line Number: 188

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/models/ver3/Contents_model.php
Line: 799
Function: get

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 605
Function: getComment

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 425
Function: initBoardView

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$benchmark is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$hooks is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$config is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$log is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$utf8 is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$uri is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$exceptions is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$router is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$output is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$security is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$input is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$lang is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$load is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$cache is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$cacher is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$jscript is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$session is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$agent is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$contentsStatus is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$articleStatus is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$db is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$member_model is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$contents_model is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$menuList is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$common is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$dto is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$together_end_date is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 387
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 557
Function: get_header

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Article_model::$best_cnt is deprecated

Filename: ver3/Article_model.php

Line Number: 18

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/models/ver3/Article_model.php
Line: 18
Function: _error_handler

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 322
Function: model

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 392
Function: getFloatingMyInfo

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 559
Function: get_footer

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Article_model::$popular_cnt is deprecated

Filename: ver3/Article_model.php

Line Number: 19

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/models/ver3/Article_model.php
Line: 19
Function: _error_handler

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 322
Function: model

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 392
Function: getFloatingMyInfo

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 559
Function: get_footer

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property Contents::$article_model is deprecated

Filename: core/Loader.php

Line Number: 353

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 322
Function: model

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 392
Function: getFloatingMyInfo

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 559
Function: get_footer

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: 8192

Message: Creation of dynamic property CI_Loader::$article_model is deprecated

Filename: core/Loader.php

Line Number: 925

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 434
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 559
Function: get_footer

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

수학동아 - 폴리매스
본문바로가기
자유게시판
수학을 주제로 떠들어 보세요!
[잡담] [제 4회 폴리매스데이] [협동 문제 풀이]
원파 2021.02.24 08:19 조회 700
공유하기
페이스북 트위터 카카오톡 카카오스토리 네이버블로그 네이버밴드

안녕하세요!

제 4회 폴리매스데이 운영진입니다.

 

지금 이 시간부터, 11시 44.5분까지 협동 문제 풀이 행사를 진행합니다.

운영진이 선정한 하나의 문제를 다양하게 접근하여 해결하면 되는데요.

시간 내에 정답이 나오지 않으면 수요일까지 연장하여 진행할 예정입니다.

 

그럼... 협동 문제 풀이의 문제, 지금 공개할게요!

 

 

가로로 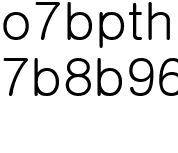n칸이며, 세로로는 무한히 긴 격자판이 존재한다.

이때, 위에서부터 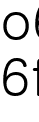m개의 줄을 바둑돌로 가득 채운다.

따라서, 격자판 위에는 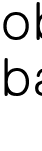n imes m개의 바둑돌이 존재하게 된다.

위에서부터 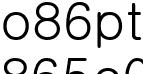i번째 줄에는 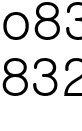i-m 이라는 번호를 매긴다. (i>m)

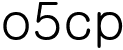이때, 한가지 시행을 할 수 있는데, 서로 상하좌우로 인접한 두 바둑돌은 하나가 하나를 넘어갈 수 있으며,

어느 바둑돌이 한 바둑돌 위를 넘어간다면 넘어가면서 지나간 바둑돌은 사라진다.

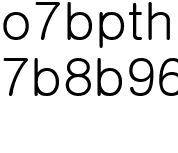n과 m은 자유롭게 정할 수 있을 때, 바둑돌을 가장 큰 번호가 매겨진 줄까지 보낸다면 이는 얼마이겠는가?

그림1은 n=8, \; m=4일때의 초기 상태를 보여주며, 그림2는 바둑돌이 서로를 넘어가는 것을 보여준다.

 

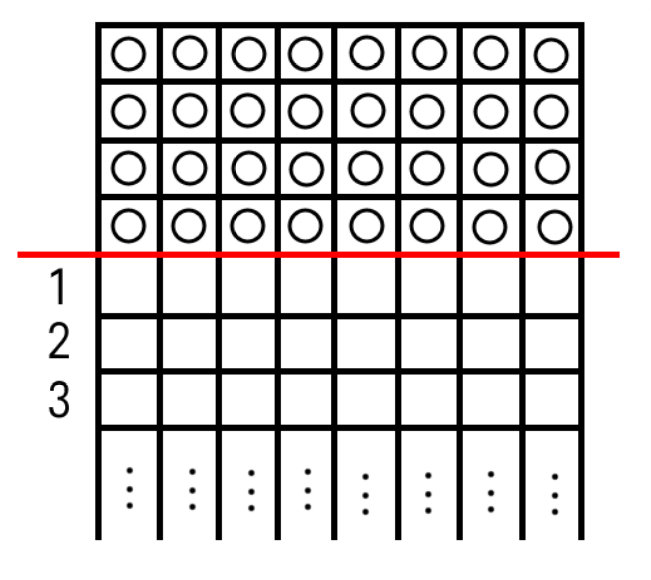
(그림1)

 

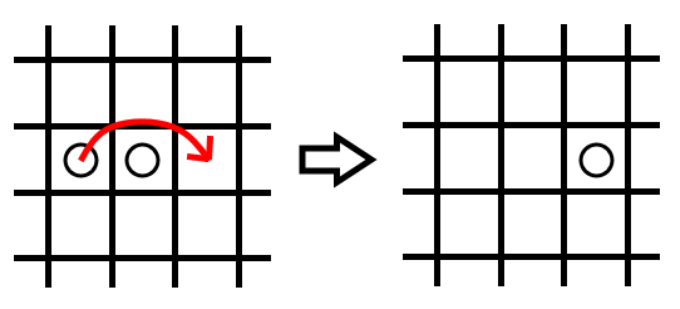
(그림2)

 

 

폴리매스 문제처럼 서로 부족한 부분을 채워가며 답에 이르러 가는 모습이 보였으면 좋겠네요!

문제는 별로 어렵지 않으니, 다양한 접근법을 고려해볼 수 있겠습니다!

 

이번 행사에는 줌 회의를 이용한 토의가 가능한데요.

공식적인 줌 회의는 11시 44.5분에 종료되나, 여러분들께서 자유롭게 사용하셔도 좋습니다.

초대 링크는 아래와 같습니다.

 

https://us04web.zoom.us/j/75873994013?pwd=RGE1OVZQV250VHY5K3FkQmEyZFBmQT09

 

회의 ID: 758 7399 4013

암호: LsJZ9r

 

그럼, 모두들 행운을 빌게요~!

추천 0 목록보기
댓글 10
댓글 작성하기
  •  
    피타구라스 Lv.9 2021.02.24 08:39

    음...어떻게 접근해야 할 지 모르겠네요...;; -.-

    일단 좀 더 고민해 보고 돌아오겠습니다...;; (그리고 줌 인원이 너무 적네요,,,슬프게도...)

    댓글 작성하기 좋아요0 댓글수1
    •  
      우럭 Lv.9 2021.02.24 08:42

      ㅠㅠ

      좋아요0
  •  
    virtual Lv.4 2021.02.24 08:55

    제가 정리한 내용으로는(줌 내용을 참고해서)

    라임님이 말한 패턴에서

    일단 바둑돌이 최대한으로 움직이려면 그 패턴이 필요할것 같은데

    패턴에서 움직이기 위한 최대거리는 m에 따라 결정될것 같고

    패턴으로 인해 더 멀리 가려면 n의 값이 중요해지죠

    여기서 n의 짝수홀수 관계에 대해 생각하고 있는데

    짝수일때로 가정할때랑 홀수일때로 가정할때는 패턴의 모양이 급격하게 변할거란 말이죠

    전 홀수일때로 생각하고 있으니 짝수일때는 다른분이 한번만 해주세요....

    댓글 작성하기 좋아요0 댓글수0
  •  
    virtual Lv.4 2021.02.24 09:15

    가정 1: n 짝수 m 짝수       가정 2: n 짝수 m 홀수     가정 3: n 홀수 m 짝수

    가정 4: n 홀수 m 홀수      가정 5 : n 홀수 m 상관없음   가정 6: n 짝수 m 상관없음

    가정 7: n 상관없음 m 홀수  가정 8: n 상관없음 m 짝수  가정 9: m,n 둘다 상관없음

    가정 10: n 무한 m 상관없음  가정 11: n 무한 m 홀수    가정 12: n 무한 m 짝수

    가정 13: 패턴따윈 없다  가정 14: m과 n이 정비례한다  가정 15: n과 m이 반비례한다

    정도로 나눌 수 있겠네요

    m이 무한이면 i가 존재할 수 없으니 안되고

    근데 출제자가 이걸 다 일일히 따지라고 낸 문제는 아닐것입니다

    이렇게 하면 패턴의 정확성을 알 수 있긴 하되,

    엄청난 노가다가 필요하죠

    전 패턴이 거의 다 비슷하다는 가정 하에 문제를 풀어보겠습니다(가정 9번)(근데 이건 아닐듯)

    일단 제가 정리한 내용으로는 현재 가정 3번을 풀고 있는데

    몇가지 경우에서는 m의 값부터 최대 (m-1)칸을 더 갈수 있다고 접근했는데

    또 그러지가 않은 경우가 있네요

    아에 패턴이 없는 경우(가정 13)의 경우로 넘어와서 지금은 생각하고 있습니다

    내일 더 자세히 정리하겠습니다

    댓글 작성하기 좋아요0 댓글수3
    •  
      원파 Lv.9 2021.02.24 09:21

      너무 n과 m에 대해서 깊이 파고 들어간 것 같아요..ㅠㅠ

      문제에서 주어진 요소는 n과 m 말고도 더 많답니다.

      다양한 요소, 관점, 접근을 통하여 문제를 풀어주길 바라요.

      다들 수학의 본질에 관하여 집착하시고 계신것 같아요.

      폴리매스 문제들은 대체로 이론에 기반하지만, 이런 관념들을 와장장 깨보라고 낸 문제입니다.

      n, m이 작은 경우에 대하여 손으로 계산해본 뒤 이를 바탕으로 규칙을 찾을지도 모르죠.

      이론적인 접근은 분명 좋은 접근은 맞지만, 너무 어렵게 접근하는 것은 오히려 문제를 어렵게 만든답니다!

      좋아요0
    •  
      virtual Lv.4 2021.02.24 09:28

      n과 m을 이용한 접근법 말고 다른게 있나요....

      이런게 바로 고정관념을 못깬 자의 질문이죠

      아 i가 있군요!

      좋아요0
    •  
      virtual Lv.4 2021.02.24 09:30

      어 m과 n을 이용한 가정 말고도 mn에 관련된 식이 하나가 생각나네요

      전체 개수에 관한 최대 높이를 구하는 방법으로 유도해야겠어요

      좋아요0
  •  
    △π Lv.9 2021.02.24 18:57

    저거 많이 알려진 문제에요

    댓글 작성하기 좋아요0 댓글수1
    •  
      △π Lv.9 2021.02.24 19:04

      각 칸에 지수가 n인 x의 단항식으로 놓고 풀면 됩니다

      좋아요0
  •  
    자몽이 Lv.6 2021.02.24 22:33

    (문제가 뭔지 못알아들은 자몽)

    댓글 작성하기 좋아요0 댓글수0
  • ㈜동아사이언스 | 등록번호 : 서울 아04396 | 등록일자 : 2017년 3월 2일 | 제호 : 동아사이언스 | 발행인 : 장경애 | 편집인 : 김민수
  • ㈜동아사이언스 폴리매스 | 대표 : 장경애 | 개인정보 보호책임자 : 주세훈(privacy@dongascience.com) | 청소년보호책임자 : 박무성
  • (03737) 서울시 서대문구 충정로 29, 10층 ｜ 문의 : 02-6749-2000 ｜팩스 : 02-3148-0809 ｜사업자등록번호 : 101-81-62201 (사업자정보확인)
  • 통신판매업신고번호 : 제2013-서울용산-01101호 ｜온라인 결제를 위한 PG사의 구매안전서비스(가입사실 확인)
  • Copyright © Dongascience. All right reserved.

  • 폴리매스 문제는 과학기술진흥기금 및 복권기금의 재원으로 운영되고, 과학기술정보통신부와 한국과학창의재단의 지원을 받아 수행된 성과물로 우리나라의 과학기술 발전과 사회적 가치 증진에 기여하고 있습니다.

  • ☎문의 02-6749-3911