함께 풀고 싶은 문제
창의력을 기를 수 있는 수학 문제 또는 퍼즐을 내는 곳입니다.
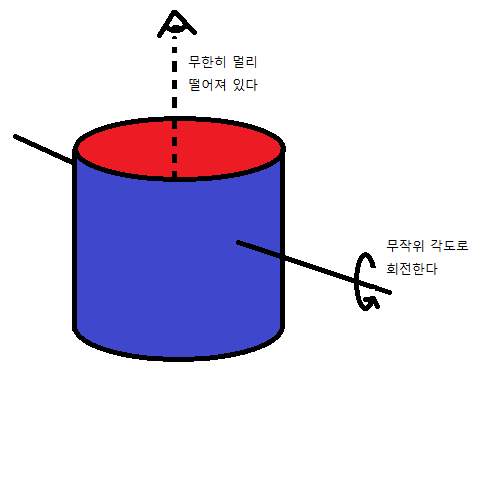
한 면에는 파랑, 반대쪽 면에는 빨강색이 칠해진 너비 h, 길이 2*pi*r이 되는 종이띠를 파랑색이 바깥쪽으로 향하도록 높이 h, 반지름 r인 원기둥의 옆면 모양으로 말았다. 이때 처음의 원기둥의 축 방향으로 무한히 먼 점에서 이것을 바라보고 있는데(시력도 무한히 좋다), 이 원기둥의 축을 수직이등분하는 직선을 축으로 0 이상, 360도 미만의 임의의 각도로 회전했다. 각의 크기와 상관없이 그 확률은 일정하다. 이때 (a)빨강색이 보일 확률과 (b)빨강색인 부분 전체에서 보이는 부분이 차지하는 비율의 기댓값을 구하시오.
이 문제 어떠셨나요?
좋아요
0
글쎄요
0
어려워요
0
닫기