폴리매스

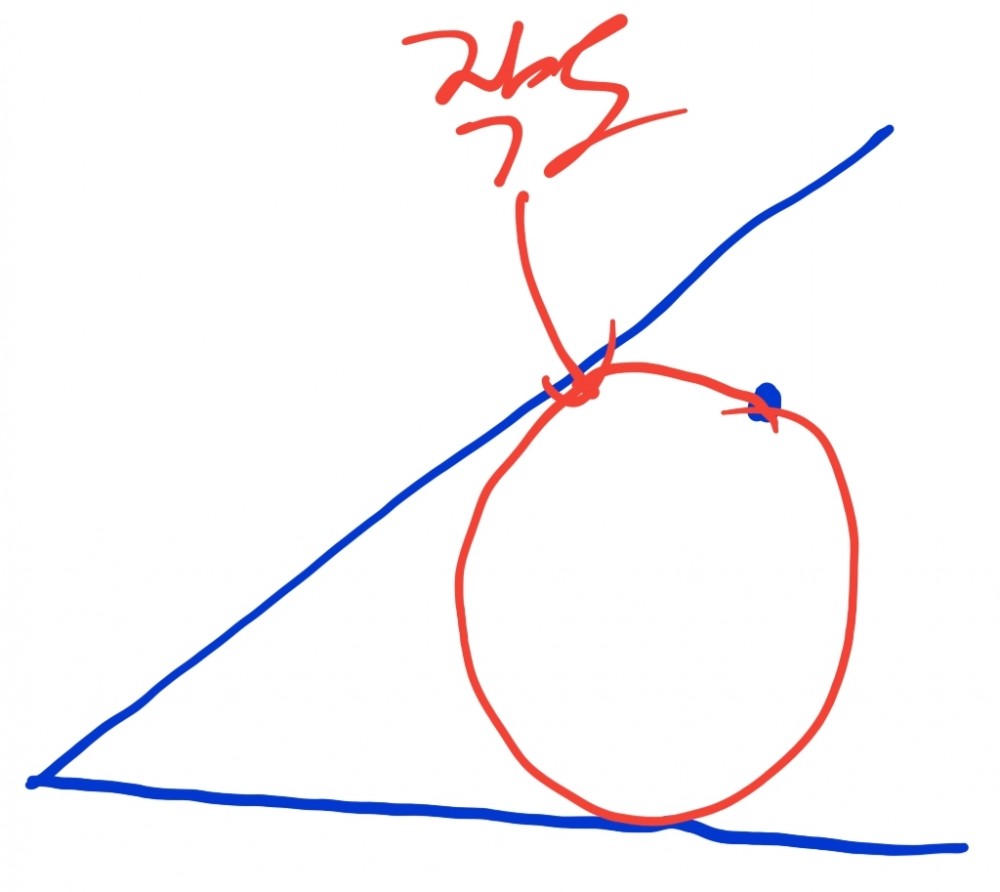
(1) 어떤 각과 그 내부에 있는 한 점이 있다. 이제 눈금없는 자와 컴퍼스로 이 점을 지나고 각에 있는 두 변에 접하는 원을 작도하여라.

(2) 이번에는 눈금없는 자는 그대로 사용이 가능하고, 컴퍼스도 사용 가능하다. 단, 컴퍼스는 고대의 컴퍼스를 사용한다. 고대의 컴퍼스는 당연히 원은 그릴 수 있으나, 컴퍼스를 드는 순간 컴퍼스 다리가 무너져서 길이는 옮길 수 없다. 이 도구들을 이용하여 정오각형을 작도하여라. 그리고 일반 컴퍼스로 작도 가능한 도형은 모두 고대의 컴퍼스로 작도 가능하다는 사실을 증명 또는 반증하여라.

(3) 이번에는 아예 컴퍼스는 사용하면 안 된다. 이제 한 선분과 그 선분의 중점, 그리고 그 선분의 연장선 위에 있지 않은 한 점이 주어져 있을 때, 그 점을 지나면서 주어진 선분과 평행한 직선을 작도하여라.