폴리매스

다음의 조건을 만족하도록 유한 개의, 길이가 같은 선분을 평면 상에 배치하는 상황을 생각하자. 

조건 1. 각 선분의 끝점은 단 하나의 다른 선분과 만난다. 

조건 2. 각 선분의 중간은 단 하나의 다른 선분과 만나며, 반드시 만나는 그 선분의 끝점과 만난다. 

여기서 선분의 '중간'은 선분의 두 '끝점'을 제외한 부분을 말한다. 

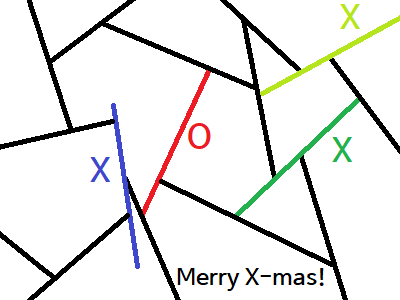
그림을 통해 조건의 의미를 살펴보자. 먼저 빨간색 선분을 보면 각 끝점에 다른 선분의 중간이 닿아 있고, 중간에는 제 3의 선분의 끝점이 닿아 있다. 즉 빨간색 선분은 조건을 만족시킨다.

하지만 연두색, 초록색, 파란색 선분은 조건을 만족시키지 않는다. 연두색 선분과 초록색 선분의 경우, 각 선분의 중간에 2개의 선분이 만나고 있다. 또, 파란색 선분의 경우 3개의 선분이 중간과 만나고 있는 것은 물론, 끝점이 아무 선분과도 만나지 않으므로 조건을 만족시키지 않는다. 

문제 0. 조건을 만족하는 배치는 평면을 볼록다각형들로 나눈다는 것을 보이자. 

문제 1-1. 조건을 만족하는 배치의 실례를 찾아보자. (힌트: 10개의 선분으로 할 수 있다.)

문제 1-2. 조건을 만족하는 배치를 이룰 수 있는 선분의 최소 개수가 무엇인지 알아내자. 

문제 1-3. 무작위로 선분들이 서로 닿지는 않도록 배치되어 있다. 이때, 선분 몇 개를 추가해 항상 조건을 만족하도록 할 수 있을까? 

수학에서는 다양한 방향으로 문제를 일반화하여 새로운 사실을 발견할 수 있다. 주어진 조건은 유지하되 다른 가정들을 바꿔보자. 

문제 2-1. 무한히 많은 선분을 허용한다면 어떤 배치가 가능하게 될지 생각해보자. 

문제 2-2. 유한한 크기의 직사각형 평면인데, 포탈처럼 좌우와 상하가 연결되어 있을 경우 어떤 배치가 가능하게 될지 생각해보자. 

문제 2-3. 2-1과 2-2를 다시 풀되, 조건을 살짝만 바꿔보자. 

변형된 조건 1. 각 선분의 끝점은 단 하나의 다른 선분과 만나며, 반드시 만나는 그 선분의 중간과 만난다. 

이제는 문제가 어떻게 되는가? 

문제 3-1. 선분들의 길이가 다를 수도 있다면 어떤 배치가 가능하게 될지 생각해보자.

문제 3-2. (문제 1-2의 변형) 이 경우는 이 경우에 선분의 최소 개수는 어떻게 되는가? 6개로 가능한 실례가 있으므로, 최소 개수는 6 이하일 것이다. 

문제 3-3. (문제 1-3의 변형) 이 경우는 선분들을 추가하여 항상 조건을 만족하도록 할 수 있는가?

고차원으로의 확장도 생각해보자. 우리가 살펴볼 수 있는 차원은 두 종류가 있다. 물체들을 놓는 곳의 차원과, 물체 자체의 차원이다. 지금까지는 2차원 평면 상에 1차원 선분을 놓았다고 할 수 있다. 

문제에 앞서, 선분에서 정의했던 '끝점'과 '중간'의 개념을 고차원으로 확장해야 한다. 길이가 1인 선분이 1차원 단위체인 것처럼, 1×1 정사각형, 1×1×1 정육면체, ...들을 각각 2차원 단위체, 3차원 단위체, ...라고 정의하자. 고차원에서는 더 이상 끝'점'이 아니라 끝'선'이나 끝'면'이 될 것이다. 정사각형의 경우 끝선은 그 둘레가 될 것이고, 정육면체의 경우 끝면은 그 표면이 될 것이다. '중간'은 역시나 '끝'을 제외한 부분이라고 정의할 수 있다. 

문제 4-1. 3차원 상에 1차원 단위체를 놓는 경우로 바꾸어 문제1-2, 문제1-3을 다시 풀어보자. 

문제 4-2. 3차원 상에 2차원 단위체를 놓는다면 어떤가? 그밖에 차원에 대해서도 생각해보자. 

문제 5. 놓이는 물체의 크기가 모두 달라도 된다고 할 때(즉, 정사각형이나 정육면체 등을 놓는 대신 직사각형과 직육면체 등을 놓는 것이다), 고차원에서의 배치를 살펴보자. 

문제 6. 그 밖의 다른 변형들도 생각해보자. 예를 들어, 두께를 추가하거나, 중력을 추가하거나, 모양을 삼각형으로 바꾸거나, 등등... 상상하는 대로 변형할 수 있을 것이다. 각 경우에 대해서 배치가 어떻게 되는지 고민해보자!!

('함께 풀고 싶은 문제'인 만큼, 저도 많은 답을 모르는 상태에서 글을 작성했습니다. 사실상 문제 0과 1-1을 제외하고는 거의 미해결입니다. 이해되지 않는 부분이 있으면 댓글 남겨주세요! 공개댓글을 통해 많은 아이디어를 공유해봅시다 ^^)