[킹앤카 9월호]
안녕하세요 수학동아입니다.
카이스트 수학문제연구회가 직접 출제하는 퀴즈킹앤카이스트 문제를 풀어보세요!
퀴즈에 참여해주신 분 중 추첨을 통해 선물을 드립니다.
한 문제만 풀어도 좋으니 여러분의 풀이를 보여주세요!
정답이 아닌 기발한 오답도 대환영입니다. 정답이 없으면 기발한 오답을 제출한 분께 선물을 드려요!
킹앤카 문제 풀이에 참여하고 싶은 분은
이 게시물의 비밀댓글로 이름, 연락처, 주소와 함께 풀이를 남겨주세요 ^^

QUIZ 1)
수지는 갑자기 “내가 정문 모양으로 재밌는 문제 하나 내볼게”라며 문제를 냈다. 만약 정문이 정사각형 7칸으로 이뤄진 아래와 같은 모양이라고 가정하면, 이 모양 7개로 7×7 격자를 채우기 위해서는 정문 모양을 자를 수밖에 없다. 그럼 최소 몇 번을 잘라야 할까?

QUIZ 2)
세 친구는 오랜만에 학교 로고를 보면서 감상에 젖었다. 이때 KAIST 글자를 보던 수지가 장난삼아 “우리 사이버 강의 들을 때 KAIST가 아니라 KAICT(Cyber Tutoring)라는 말도 있었는데, 수학적으로 보면 KAICT 로고가 더 맞는 것 같은데?”라고 했다. 이 말은 무슨 뜻일까?
QUIZ 3)
세 사람은 학생 식당에서 밥을 먹기로 결정하고 캠퍼스 지도를 봤다. 학생 식당은 세 곳이고, 정문과의 거리는 동측이 225m, 서측이 750m, 북측이 575m다. 세 명은 어디로 가면 가장 빨리 밥을 먹을 수 있는지 내기했는데, 의진은 동측을, 경희는 서측을, 수지는 북측을 골랐다. 단, 동측은 음식이 나오는 데 10분 걸리고, 서측은 5분, 북측은 6분이 걸린다. 그리고 세 명은 식당까지 자전거를 타거나 걸어갈 수 있다. 걸을 때는 1분에 50m, 자전거는 1분에 150m를 갈 수 있으나 탈 준비와 주차에 5분이 걸린다. 자전거를 탈 경우와 걸어갈 경우, 각각 누가 선택한 곳을 가야 음식을 빨리 받을 수 있을까?
-
-
비밀 댓글이 등록 되었습니다.댓글 작성하기 댓글수0
-
-
-
-
-
-
-
2번만에 되지 않나요?
1112223
1112223
3144255 3
3444555 3/3/3
3644755 3/3/3
6667773
6667773
-
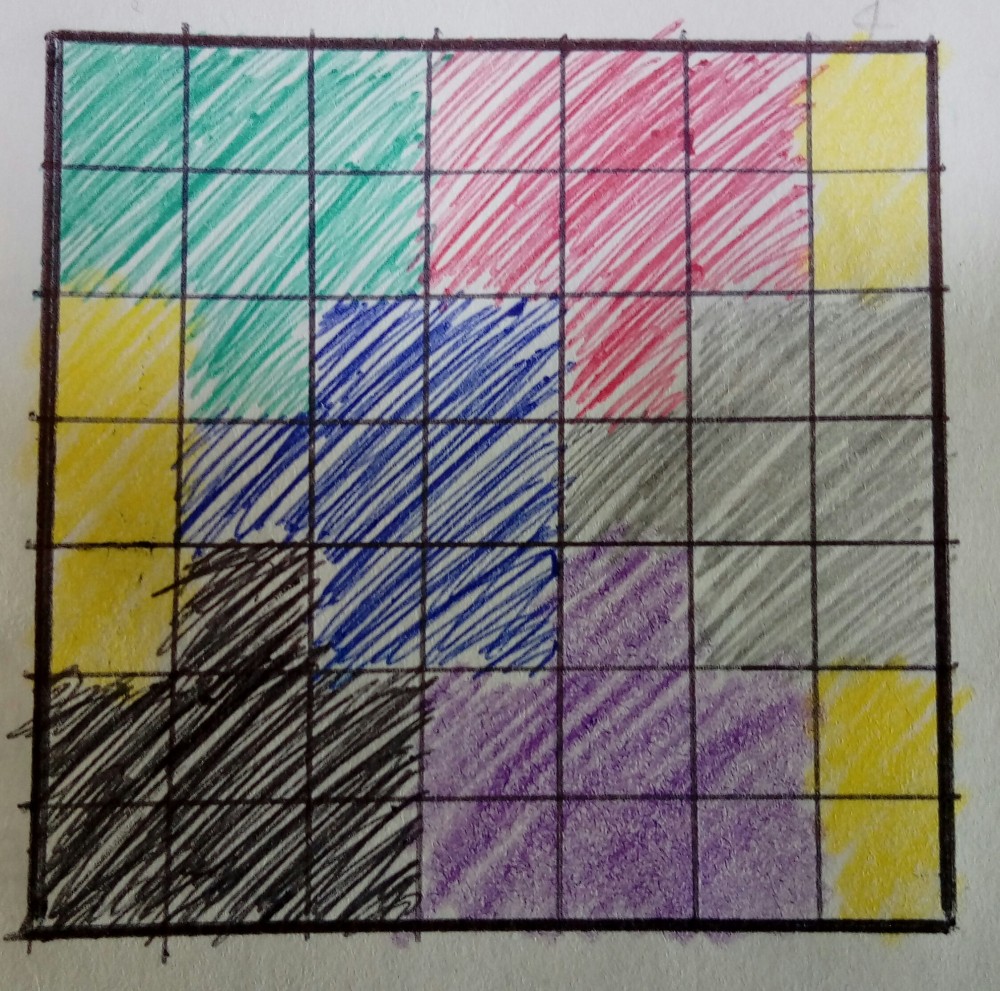
황냥이님께서 말씀하신 것처럼 1번 문제에서 위의 그림처럼 채우면 2번만 자르고 채울 수 있습니다.
또한, 1번 이하로 잘라 채우는 것이 가능하다고 가정하겠습니다. 1번 이하로 자를 경우 원래 모양과 다른 조각이 2개 이하입니다. 7×7격자의 네 꼭지점 모두가 원래 모양과 다른 조각으로 덮인다면 한 조각은 3칸 이상 떨어진 두 칸을 덮을 수 없으므로 2개보다 많은 조각이 필요해집니다. 그러므로 네 꼭짓점 중 적어도 하나는 원래 모양으로 덮이며, 회전대칭이므로 이것을 왼쪽 위 꼭짓점이라고 해도 일반성을 잃지 않습니다. 왼쪽 위부터 격자의 칸을 행렬로 보겠습니다. (1,1)은 자르지 않은 조각으로 덮여 있으며 이것을 덮는 두 가지 방법이 서로 대칭이므로 일반성을 잃지 않고 (1,1)을 덮은 조각이 (1,1)(1,2)(1,3)(2,1)(2,2)(2,3)(3,2)를 덮었다고 하겠습니다. 이때 (3,1)은 자르지 않은 조각으로 덮을 수 없게 되므로 잘린 조각 하나가 (3,1)을 덮어야 합니다. 자르지 않은 조각으로 (1,4)를 덮는 방법은 두 가지가 있으며 두 가지 방법 모두 (2,6)을 덮게 됩니다. 그러므로 (1,4)를 자르지 않은 조각으로 덮는다면 (2,7)은 잘린 조각으로 덮어야 합니다. 즉, (1,4)또는 (2,7)은 잘린 조각으로 덮입니다. 또한 이것은 (3,1)을 덮은 조각과는 다르므로 두 개의 잘린 조각을 모두 사용했습니다. (7,1)을 자르지 않은 조각으로 덮는 방법은 두 가지가 있으며 두 방법 모두 (6,3)을 덮습니다. (7,4)를 자르지 않은 조각으로 덮으며 (6,3)은 덮지 않는 방법은 두 가지가 있으며 두 방법 모두 (6,6)을 덮습니다. 이때 자르지 않은 조각으로 (7,7)을 덮으며 (6,6)을 덮지 않을 수는 없습니다. 그러므로 (7,1)(7,4)(7,7)중 하나는 잘린 조각으로 덮이는데 한 조각이 3칸 이상 떨어진 두 칸을 덮을 수 없으므로 이것 중 하나를 덮는 잘린 조각은 위에서 사용한 잘린 조각과는 다른 조각이고, 이는 잘린 조각이 2개 이하임에 모순입니다. 따라서 1번 이하만 잘라서 7×7 칸을 모두 덮을 수 없으며, 자르는 최소 횟수는 2번이 됩니다.