일단풀이
4번풀이
최대공약수의 성질의 따라
gcd(n, n+1) = gcd(n, n+1-n) = gcd(n, 1) = 1이다
또,
gcd(n, mn+1) = gcd(n, mn+1-n) = gcd(n, mn+1-n-n) = ... = gcd(n, 1) = 1
이걸또 바꾸면 서로 서로소인정수의 꼴은
gcd(n, mn+1)임을 알수있다
따라서 a,b의꼴은
gcd(a, ma+1)또는 gcd(mb+1, b)꼴임임을 알수있다
이것을 무한 개념으로 확장시켜보자
m을 무한으로 보내면...
집합의 밀도의 정의의 따라
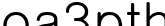 에서 m = t임으로 둬도 무방하다
에서 m = t임으로 둬도 무방하다
따라서 문자순서쌍을 나열하면
a, a+1
a, 2a+1
a, 3a+1
.
.
.
a, ta+1
즉, 이것의 순서쌍은 t개이고
a는 미지수이므로a가 각각 다른수일때 경우를 고려해야되므로 곱의 법칙(데카르트곱)의의해 a를 또 무한으로 두면 t로 봐도되므로
t^2이다
그리고
다른조건인 b에대해
b+1, b
2b+1, b
.
.
.
tb+1, b
여기서도
t^2개
이제 두경우를 합의법칙(독립변수합)으로 합하면 2t^2
따라서 이값을 집합의 밀도정의에 대입하면
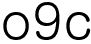
5번문제풀이
이번엔 차원을 이용해볼겁니다
N^n을 자른 (R^n 공간으로 볼수있다)
평면을 이용하여
4번문제에서 유도할겁니다
평면을 나눌경우의수는
어떤 2가지의 a_i들을 묶어야됩니다
곱의법칙의 의해 a_i들의 순서쌍은 모두 n(n-1)개네요
일단 4번문제에서 서로소일수는 t^2이라고했습니다
이제 이것들이 서로소인 gcd묶음 ex) gcd(a_i, a_k) = 1인 1개이상의 것들만 있으면 됩니다
이항정리 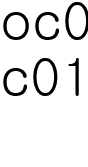 를 변형해
를 변형해 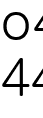 을 대입하면
을 대입하면 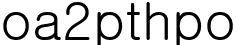
따라서 조합의 정의에 의해 어느 수의 n이하 0이상의 묶음을 택하는 경우의수와같다
하지만 우리는 1개이상만이 필요하므로
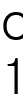 로 0을 제외한다
로 0을 제외한다
따라서 우리가 구하는식은 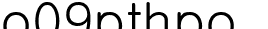 이고
이고
이것을 집합의 밀도에 대입하면  이다
이다
이를 미분해보자
n을 매개변수로 하자
지수함수미분법과 합성함수미분법의의해 2^n+1*ln 2이다
1/n을 리만적분해보자
ln n이된다
그러면 제타함수 꼴이된다
제타함수도 무한 합으로 적분과같은 ln n의 근사값을 가진다
따라서 ln 2에
제타함수를 적분한것을 변형한것을 대입하고
다시 n을변수로 리만적분하면
 이 다시나온다
이 다시나온다
근데(밤 10시쯤에해서 정신이 이상해서그런걸수도(?) 주말중에 한번더 도전해봅니다)










