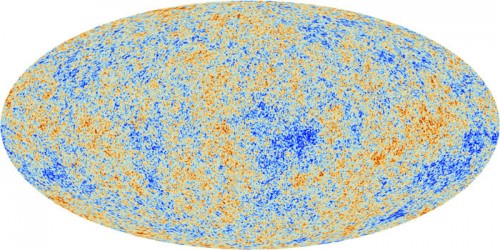
동수는 서로 합동인 정삼각형 4개 이상으로 다면체를 만들었다. 그런데 개수가 부족해 삼각형 모양의 빈칸이 생기고 말았다. 다면체의 어떤 세 꼭짓점도 한 직선 위에 있지 않도록 만들었다고 한다. 동수는 같은 조각 하나만 더 있으면 항상 다면체를 완성할 수 있을까?
좋아요
0
글쎄요
0
어려워요
0
-
-
어떤 꼭짓점도 한 직선 위에 있는건 불가능 하니 3꼭짓점이라고 생각을 하고, 풀어보면, 꼭 삼각형 모양이 작은 삼각형일 필요는 없으니 크게 나오는 경우도 고려하면 불가능 하다. 맞나요..??
그냥 머릿속으로만 생각해서... 라고 적었습니다.
또, 디두유님이 말씀해주신 그 부분은 제가 잘못 생각했을 수 도 있지만, 2개의 꼭짓점은 무조건 한 직선위에 놓이므로 3꼭짓점이라고 생각했습니다.
-
확인요청중비밀 댓글이 등록 되었습니다.댓글 작성하기 댓글수7
-
뭐라고 적었나요?? 궁금해서요 .. 혹시 일반댓글로 새로 달아주실 수 있나요??
좋아요0 -
확대하거나 축소하면 같아지니까 변의 길이는 관련이 없지 않나요?
좋아요0 -
아 죄송합니다. 자동으로 비밀댓글 설정이 되있었네요ㅡ.ㅡ
다시 올리겠습니다.
좋아요0 -
모두 합동인 정삼각형이니까 안돼지 않나요?
좋아요0 -
오히려 모두 합동이니까 똑같이 변의 길이가 1에서 2가 되면 전체가 2배 늘어나게 해 같게 만들 수 있을 것 같습니다.
또, 변의 길이가 1일 때도 '당연히'가 아닐 수도 있어요!
좋아요0 -
글쎄요. 변의 길이가 2라면 밑에 경우 밖에 안되지 않나요?
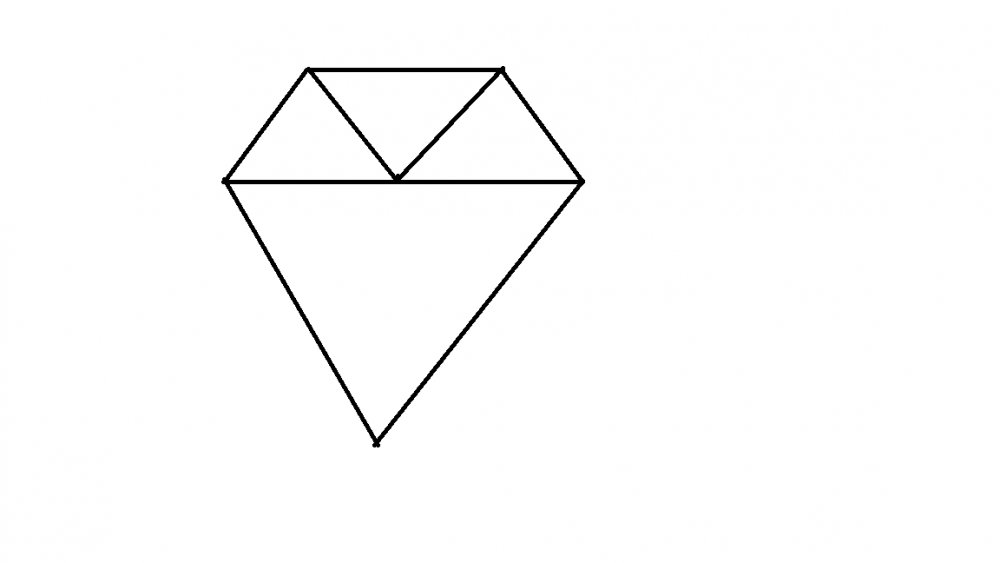 좋아요0
좋아요0 -
저 큰 삼각형이 빈칸이라고 하시는 거라면, 그 변에 붙어 있는 세 점이 한 직선 위에 있게 되어 조건에 어긋납니다!
좋아요0
-
-
해결비밀 댓글이 등록 되었습니다.댓글 작성하기 댓글수2
-
가능 하다고 생각합니다. 삼각형 조각의 한 변의 길이가 1이라고 가정할 떄, 한 변의 길이가 1인 삼각형 모양의 구멍이면 당연히 가능하고 한 변의 길이가 2인 경우, 한 변을 이루는 두 변에 각각 삼각형을 붙이면 두 삼각형 사이에 빈칸이 생기고,
그 빈칸을 삼각형으로 메울 수 있는 경우는 3개의 삼각형이 모두 한 평면 상에 있는 경우 뿐입니다. 그렇게 되면 처음에 가정했던 한 변의 길이가 2인 삼각형 모양의 구멍의 한 변에 3개의 꼭짓점이 모두 한 직선 상에 있게 됩니다.
같은 이유로 변의 길이가 3이상인 경우도 불가능 합니다.
그러므로 언제나 남은 구멍은 한 변의 길이가 1이므로 가능합니다.