함께 풀고 싶은 문제
창의력을 기를 수 있는 수학 문제 또는 퍼즐을 내는 곳입니다.
[창의 퍼즐] [억지논리]야우심통의 억지논리 시즌 2 27탄
페렐만 : 심통아! 수학동아에 '매스포터'가 생겼데!
야우심통 : 오호 짝퉁 페이지를 만들어서 폴리매스 회원들을 모두 데리고와야겠군!
페렐만 : 그럴 일은 없을 듯... 어쨌거나 내가 기사를 썼는데 좀 봐줘
http://www.polymath.co.kr/article/view/70
야우심통 : 음...근데 좀 이상한데?
페렐만 : 치과 가봤어?
야우심통 : ...요새는 왜 너랑 나랑 역할이 바뀐 거 같지
페렐만 : 벌써 야우심통의 억지논리 27탄인데, 서당개 삼년이면 풍월을 외운다고 나도 억지논리 하나 정도는 만들 수 있지...
야우심통 : 그래...그래서 오늘의 억지논리는 뭐지?
페렐만 : 앗 그건 내 대사인데...
기사를 잘 보면
n문제 중 r문제를 맞힐 확률 =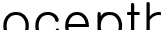 
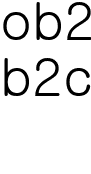일 것입니다. 왜냐하면, 전체 문제 중 r문제를 맞히는 일과 n-r개를 틀리는 일이 동시에 일어나는 확률이기 때문입니다. 자, 그러면 10문제 중에서 r문제를 맞힐 확률을 알아볼까요?
| r개 | 0개 | 1개 | 2개 | 3개 | 4개 |
| 확률 | 10.7% | 2.7% | 0.7% | 0.2% | 약 0.00% |
(모든 확률은 소수점 아래 2번째 자리에서 반올림하여 나타냈습니다.)
이런 부분이 있지? 근데 잘 보면 r이 커질수록 확률은 작아진다구! 그러면 확률의 합이 100이 되지 않을 거라구!(기사에서 r이 10이하라는 제약이 있습니다)
야우심통 : ??
이 문제 어떠셨나요?
좋아요
0
글쎄요
2
어려워요
1
닫기
