주니어 폴리매스를 시작하면서 아주대 수학과 방승진 교수님은 다음과 같은 조언을 해주셨습니다. 앞으로 교수님의 의견에 따라 문제를 풀어 보세요!
요즘 수학 문제는 일회용 물수건처럼 쓰고 버리는 것이라는 인상을 지울 수 없습니다. 학생들은 셀 수 없을 정도로 많은 수학 문제를 풀고 또 풀지만 수학 실력은 늘어나지 않습니다. 왜 일까요? 머리가 나빠서 일까요? 연구에 따르면 학생들은 누구나 잠재력이 있다고 합니다. 수학도 마찬가지 아닐까요?
제 경험에 의하면 수학 문제를 마치 껌 씹듯이 생각에 생각을 거듭하면 다양한 생각을 하게 되고 어느 덧 그 수학 문제는 영원히 잊지 않을 정도로 친숙하게 됩니다. 좀 더 정확하게 "어떤 문제를 푸는가도 중요하지만 문제를 어떻게 푸는가?" 가 더 중요합니다. 결국 문제를 풀고 난 뒤에 '어떤 창의적인 산출물을 만들었는가?' 가 중요합니다.
앞으로 게재하는 문제들은 주로 다양하게 생각하도록 유도하는 문제 즉, 개방형 문제(open-ended problem)로서 여러분들이 좀 더 창의적인 태도를 가질 수 있도록 안내할 겁니다.
모든 문제는 주어진 질문에 국한하지 말고 될 수 있는 한 일반화 시키고, 남들과는 다르게 생각하려고 노력해야 좋습니다. 수학 논문을 쓰면 더욱 좋습니다.
문제 <그림 2>에서 원이 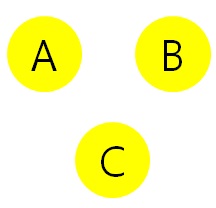 의 모양으로 놓인 곳은 어디나 A와 B의 차가 C가 된다. 또 6개의 ○안에는 1에서 6까지의 정수가 모두 한 번씩 들어가 있다. 이 규칙에 따라 <그림2>처럼 맨 아래 ○안에 숫자가 3일 때, 10개의 ○안에 1에서 10까지의 정수를 한 번씩만 사용해서 채워라.
의 모양으로 놓인 곳은 어디나 A와 B의 차가 C가 된다. 또 6개의 ○안에는 1에서 6까지의 정수가 모두 한 번씩 들어가 있다. 이 규칙에 따라 <그림2>처럼 맨 아래 ○안에 숫자가 3일 때, 10개의 ○안에 1에서 10까지의 정수를 한 번씩만 사용해서 채워라.
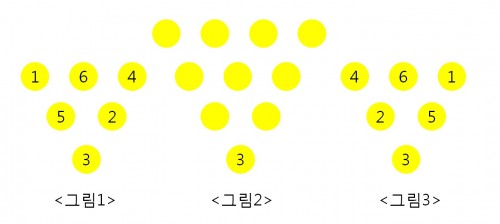
이런 경우를 4가지 찾고, 3 대신 다른 수를 써도 되는지도 조사하여라. .
-
1-1은 많이 도전을 해보았으나 안되서 일단 패스....
1-2를 보면 일단 10은 1~9 중에서 그 어느 수의 차로도 나타낼 수 없으니 불가능하고,
9는 10 - 1의 경우만 가능한데, 이 역시 10을 그 어느 수의 차로 나타낼 수 없으니 불가능하고,
8은 10 - 2와 9 - 1의 경우만 가능합니다. 그러나 10 - 2는 위의 이유와 같은 이유로 불가능하고, 9 - 1의 경우는 9가 10 - 1의 경우로만 가능한데 1을 이미 써버렸기 때문에 불가능하고,
7은 10 - 3, 9 - 2, 8 - 1의 경우만 가능합니다. 그러나 10 - 3은 불가능하고, 9 - 2는 위의 이유과 같은 이유로 불가능하고.........
요롷게 해보면 4에서 가능한 거 같은데.......(위에서부터 8, 10, 3, 9, 2, 7, 6, 5, 1, 4)
저도 헷갈리니깐 제가 미쳐 못 봤거나 잘못된 부분은 지적해주세요!!
-
이어서 계속 해보면 6에서는 7 1, 8 2, 9 3이 가능한데(10 은 어차피 안돼니까 빼겠습니다.) 7은 또 8 1. 9 2 인데 1은 이미 써서 안돼고 9 2에서 9는 10 1이지만 10을 써서 안됍니다.
그리고 5인 경우는 6 1,7 2,8 3,9 4입니다. 6은 7 1, 8 2, 9 3인데 1은 써서 안돼고,8도 9 1인데 불가능하고 9는 10 1이므로 불가능합니다.
4인 경우는 코딩의 달인님께서 말씀해주신 것처럼 되고,3인 경우도 있습니다.
밑이 2인 경우에는 9 7, 8 6, 7 5,6 4,5 3,3 1이 있는데 9,8은 위 경우처럼 불가능합니다.더 계산을 해야겠네요!
좋아요0
-
-
-
-
-
그럼 맨 아래가 1인것도 한 번 봅시돱!
그리고 교수님이 말씀하시길 문제를 일반화 하는 것도 좋은 방법이라고 하시니
일반화에 대해서도 같이 고민해 봅시다.
저도 조금(진짜 조금) 고민해 봤는데, 맨 아래가 n이라고 하면,
그 위에에 올 수 있는 경우의 수는 9 - n(어차피 10이 오면 안되니까 미리 하나 빼놓을께요)인데, 그 위에꺼는 제 머리에 한계가 왔네요..
그리고 제 생각에는 맨 아랫줄부터 세 번쨰 줄까지 6개로 이루어진 역삼각형 있잖아요 거기에 1, 2, 3이 다 들어가면 삼각형 만들기가 불가능 한 거 같은데..
혹시 제가 틀린 부분이나 잘못된 부분이 있다면 꼭! 알려주세요!
-
그럼 한번 지금까지 한 것 좀 정리해 봅시다.
1 - 1은
8 10 1 6 6 1 10 8 6 10 1 8 8 1 10 6
2 9 5 5 9 2 4 9 7 7 9 4
7 4 4 7 5 2 2 5
3 3 3 3
요롷게 해서 된 것 같구요
1 - 2를 보면
10, 9, 8, 7, 6, 5는 불가능하다는 것에 증명됬고, 4, 3, 2 는 가능합니다. 그러나 1은 아직까지 증명이 되지 않았습니다!
우리모두 힘내서 이거 끝내고 정사각형 채우기로 갑시다!!!
-
-
1 - 1은
8 10 1 6 6 1 10 8 6 10 1 8 8 1 10 6
2 9 5 5 9 2 4 9 7 7 9 4
7 4 4 7 5 2 2 5
3 3 3 3
요롷게 해서 된 것 같구요
1 - 2를 보면
10, 9, 8, 7, 6, 5, 1는 불가능하다는 것에 증명됬고, 4, 3, 2 는 가능합니다. 요게 답인가요?
좋아요0 -
그런데 뭔가 찝찝하네요... 각 숫자들을 문자들로 바꿔서 왜 안되고, 왜 되는지도 증명을 해야하지 않을까요?
좋아요0 -
밑이2도 불가능하지않나요?
좋아요0 -
제가 계산한 결과 1,2 는 불가능하다는 결론이 나오네요.
그럼 9.8.7.6.5.2.1은 불가능하고 3.4는 되는 것 같네요!
좋아요0
-
-
-
-
저는 초등학교 2학년 입니다.
처음 이 사이트에 들어와서 수학퍼즐을 해 보았는데 너무 재미있었답니다.
제가 해 본 정답은
6 10 1 8
4 9 7
5 2
3
-
자 정사각형 채우기는 끝났으니깐 우리 이거래도 열심히 해봅시다! (할게 이거밖에 없음..)
근데 여기 왜 이렇게 썰렁한걸까요?
-
1-1. 아래와 같은 4가지 경우입니다.
8 10 1 6 2 9 5 7 4 3
6 1 10 8 5 9 2 4 7 3 6 10 1 8 4 9 7 5 2 3 8 1 10 6 7 9 4 2 5 3
1-2. 4를 사용하면 4가지가 가능합니다.
8 3 10 9 5 7 1 2 6 4
8 10 3 9 2 7 6 5 1 4 9 3 10 8 6 7 2 1 5 4 9 10 3 8 1 7 5 6 2 4
프로그램을 이용해 확인해본 결과 더 이상의 방법은 없었습니다.
소스 코드
#include <bits/stdc++.h> int board[10][10]; bool chk[20]; int main(){ for(int i=1; i<=10; i++){ for(int j=1; j<=10; j++){ if(i==j) continue; for(int k=1; k<=10; k++){ if(i==k||j==k) continue; for(int l=1; l<=10; l++){ if(i==l||j==l||k==l) continue; board[1][1] = i; board[1][2] = j; board[1][3] = k; board[1][4] = l; chk[i] = chk[j] = chk[k] = chk[l] = 1; for(int ii=2; ii<=4; ii++){ for(int jj=1; jj+ii<=5; jj++){ board[ii][jj] = abs(board[ii-1][jj] - board[ii-1][jj+1]); if(chk[board[ii][jj]]) goto next_t; chk[board[ii][jj]] = 1; } } for(int ii=1; ii<=4; ii++){ for(int jj=1; jj+ii<=5; jj++){ printf("%d ", board[ii][jj]); } puts(""); } puts(""); next_t: for(int i=1; i<=10; i++) chk[i] = 0; } } } } }
-
-
-
5일때 위에서부터 2 10 9 6 8 1 3 7 2 5 이면 가능하지 않나요? 오류 있으면 얘기 해 주세요
-
-
-
확인요청중
제 답은 반대로 있는게 2개 있어서 진짜로는 2개만 구한 거에요.
8 10 3 9 9 3 10 8 9 10 3 8 8 3 10 9
2 7 6 6 7 2 1 7 5 5 7 1
5 1 1 5 6 2 2 6
4 4 4 4
-
확인요청중
전체10개 구멍의 삼각형이지만
6개 구멍의 삼각형으로 쪼갠후
그것의 패턴을 찾았습니다
a3,a4,a5
a1,a2
a0
그러면 a0=|a1-a2|=|a3-a5| 라는 패턴이
항상 성립할 것 같아요
이것을 증명한다면?
더 큰 삼각형에도 일반화 시켜싴
뭔가 해볼 수 있을거 같아요
-
확인요청중
전체10개 구멍의 삼각형이지만
6개 구멍의 삼각형으로 쪼갠후
그것의 패턴을 찾았습니다
a3,a4,a5
a1,a2
a0
그러면 a0=|a1-a2|=|a3-a5| 라는 패턴이
항상 성립할 것 같아요
이것을 증명한다면?
더 큰 삼각형에도 일반화 시켜싴
뭔가 해볼 수 있을거 같아요
-