함께 풀고 싶은 문제
창의력을 기를 수 있는 수학 문제 또는 퍼즐을 내는 곳입니다.
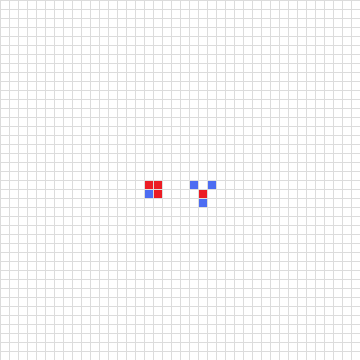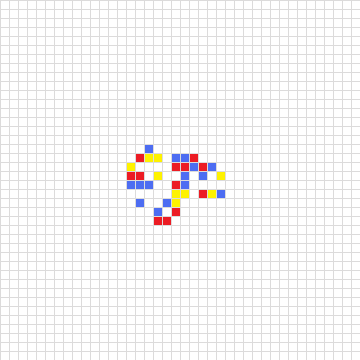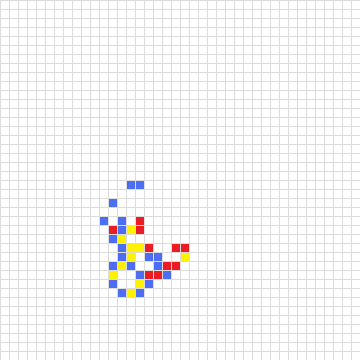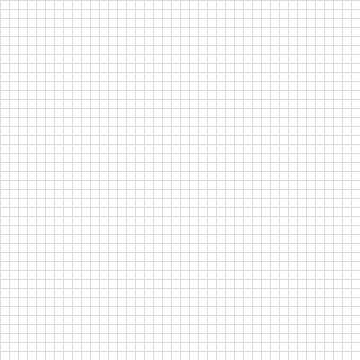
무한히 넓은 정사각형 격자가 있다. 여기에 붉은색, 푸른색의 칸을 유한 개 칠한다. 칠하지 않은 칸은 모두 흰색이다. 그리고 매 시행마다 다음과 같은 일을 한다.
(1) 푸른색 칸과 변을 맞댄 흰 칸을 푸르게 칠한다.
(2) 붉은색 칸과 변을 맞댄 흰 칸을 붉게 칠한다.
(3) n개의 푸른 칸과 변을 맞댄 푸른 칸을 붉게 칠한다.
(4) n개의 붉은 칸과 변을 맞댄 붉은 칸을 희게 칠한다.
(5) 붉은색과 인접한 푸른색 칸은 붉게 칠한다.
위 일의 우선순위는 번호 순이다. n이 몇일 때 유한 번의 시행 안에 같은 모양이 무한히 반복해서 나올 수 있는가?
이 문제 어떠셨나요?
좋아요
0
글쎄요
0
어려워요
0
댓글 6
댓글 작성하기
-
최근에 생명 게임에 관심을 가지게 되었고, 예전에 폴리매스에 올라온 이 문제가 생각나서 풀어보려고 합니다.
시행 (1)~(5)의 우선순위가 번호 순이라고 했는데, 이는 (1)을 실행해서 다음 세대를 얻고, 그 상태에서 (2)를 실행해서 다음 세대를 얻고, ... 이러한 과정을 의미하는 것인가요?
아니면 현재 세대에서 (1)에 해당하는 칸, (1)에 해당하지 않지만 (2)에 해당하는 칸, (1),(2)에 해당하지 않지만 (3)에 해당하는 칸, ...를 구하고 한 번에 다음 세대를 계산하는 것인가요?
또, (5)에서 '인접한'은 대각선을 포함하나요?
-
해결비밀 댓글이 등록 되었습니다.댓글 작성하기 댓글수0
닫기
