국가수리과학연구소 28번
은 동전을 사수하라!
문제 출제자 : 백진언 수리과학연구소 연구원
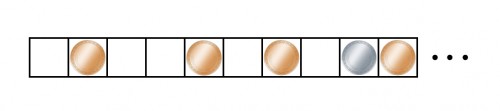
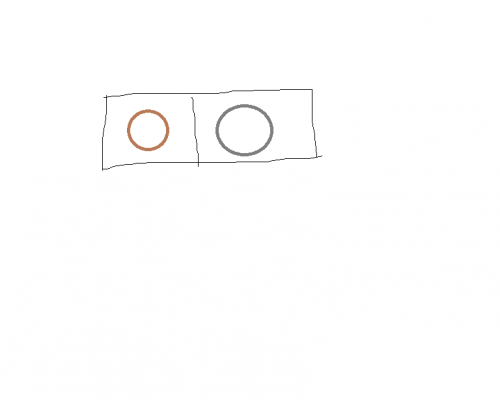
위 그림처럼 모눈종이 한 줄 위에 1개 이상의 동전이 있다. 동전들 중 1개만 은으로 만든 동전이고 나머지는 동으로 만들었다. 두 사람이 번갈아가며 아래 규칙 중 하나의 동작을 한다.
①맨 왼쪽 동전을 가져간다. ②한 동전을 다른 동전을 넘지 않고 왼쪽으로 원하는 칸만큼 옮길 수 있다. 이때 반드시 한 칸 이상 옮겨야 한다.
[문제]
은으로 만든 동전을 가져간 사람이 게임에서 이길 때 처음 하는 사람이 이길 수 있는 동전 배치 조건은 무엇일까? 단, 두 사람이 최선을 다해 플레이 한다.
★축하합니다!★
국가수리과학연구소 28번 문제에 관심 가져 주셔서 감사합니다.^^ 파스칼 학생이 많은 친구들의 도움을 받아 문제를 해결했어요! 축하합니다.^^
-
이 문제에서는 "끝나지 않는 배치"가 있을 것 같습니다.
단순히 동 동전 하나가 왼쪽에 있고 은 동전이 오른쪽에 있다면, 게임은 절대로 끝나지 않겠죠.
-
A PHP Error was encountered
Severity: Warning
Message: mkdir(): Permission denied
Filename: libraries/Common.php
Line Number: 202
Backtrace:
File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 202
Function: mkdirFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 236
Function: getLatexImgFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/view_comment_list.php
Line: 90
Function: parseLatexImgFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/view.php
Line: 343
Function: viewFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 558
Function: viewFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_onceA PHP Error was encountered
Severity: Warning
Message: file_put_contents(/DATA/upload/polymath/latex/692fae5546961d1c5f32c4b2f93d271c.gif): failed to open stream: No such file or directory
Filename: libraries/Common.php
Line Number: 213
Backtrace:
File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 213
Function: file_put_contentsFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 236
Function: getLatexImgFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/view_comment_list.php
Line: 90
Function: parseLatexImgFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/view.php
Line: 343
Function: viewFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 558
Function: viewFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_onceA PHP Error was encountered
Severity: Warning
Message: mkdir(): Permission denied
Filename: libraries/Common.php
Line Number: 202
Backtrace:
File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 202
Function: mkdirFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 236
Function: getLatexImgFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/view_comment_list.php
Line: 90
Function: parseLatexImgFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/view.php
Line: 343
Function: viewFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 558
Function: viewFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_onceA PHP Error was encountered
Severity: Warning
Message: file_put_contents(/DATA/upload/polymath/latex/587e6b2773daecf819f99ed5db05365a.gif): failed to open stream: No such file or directory
Filename: libraries/Common.php
Line Number: 213
Backtrace:
File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 213
Function: file_put_contentsFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 236
Function: getLatexImgFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/view_comment_list.php
Line: 90
Function: parseLatexImgFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/view.php
Line: 343
Function: viewFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 558
Function: viewFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_onceA PHP Error was encountered
Severity: Warning
Message: mkdir(): Permission denied
Filename: libraries/Common.php
Line Number: 202
Backtrace:
File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 202
Function: mkdirFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 236
Function: getLatexImgFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/view_comment_list.php
Line: 90
Function: parseLatexImgFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/view.php
Line: 343
Function: viewFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 558
Function: viewFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_onceA PHP Error was encountered
Severity: Warning
Message: file_put_contents(/DATA/upload/polymath/latex/587e6b2773daecf819f99ed5db05365a.gif): failed to open stream: No such file or directory
Filename: libraries/Common.php
Line Number: 213
Backtrace:
File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 213
Function: file_put_contentsFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/libraries/Common.php
Line: 236
Function: getLatexImgFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/view_comment_list.php
Line: 90
Function: parseLatexImgFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/view.php
Line: 343
Function: viewFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Contents.php
Line: 558
Function: viewFile: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once시간이 많이 없어서 제대로 증명하거나 하지는 않았지만 다른사람에게 힌트가 되기를 빌며 적어보도록 하겠습니다.
먼저 이게임과 님게임이 비슷하다고 생각해 보았습니다. 님게임의 경우 게임을 설계하기 위해서 한 턴동안 남이 가져간 돌과 내가 가져간 돌의 수의합이 일정하도록 게임을 진행합니다. 이 문제에서도 게임을 설계하기 위한 '키'를 설정해야 한다고 생각했습니다. 그리고 전 그 키로 움직이는 돌의 칸 수의 합이 짝수나 홀수가 되어야 한다고 생각했습니다( 이부분은 게산해보면서 홀순지 짝순지 알아보아야 겠지만 짝수로 예상) 그리고, 님게임에서 돌의 갯수는 여기서 돌이 움직일 수 있는 최대 갯수로 보았습니다. 맨 왼쪽에서 돌n 개가 각각
 의 위치해 있다고 한다면 모두 한칸씩 움직이고 더이상 움직일 수 없을때 제거되는 횟수까지 친다면 총
의 위치해 있다고 한다면 모두 한칸씩 움직이고 더이상 움직일 수 없을때 제거되는 횟수까지 친다면 총  가 되겠죠. 여기서 돌이 n 칸 움직인다면
가 되겠죠. 여기서 돌이 n 칸 움직인다면  개의 돌에서 n 개의 돌을 가져간다고 비유한다고 할수 있겠습니다. 돌이 제거되는 경우는 제거되는 위치를 고려해서 몇번 움직일수 있었는지 본다면 이 경우도 몇개의 돌을 가져갔다고 비유할 수도 있을 겁니다. 이렇게 님게임과 비교를 해보며, 이 문제는 돌의 움직임에도 제한이 있으니 이도 생각하면서 풀면 될것 같습니다.
개의 돌에서 n 개의 돌을 가져간다고 비유한다고 할수 있겠습니다. 돌이 제거되는 경우는 제거되는 위치를 고려해서 몇번 움직일수 있었는지 본다면 이 경우도 몇개의 돌을 가져갔다고 비유할 수도 있을 겁니다. 이렇게 님게임과 비교를 해보며, 이 문제는 돌의 움직임에도 제한이 있으니 이도 생각하면서 풀면 될것 같습니다. 막 쓴글이라 오타, 잘못 생각한 부분이 있을 수도 있으니 내 생각과 뭔가 다른것 같다? 하면 바로 질문해 주시면 감사할 것 같습니다.
-
조건 2에서 한 동전이 다른 동전을 넘지 않고 라는
이야기가 서로 겹쳐지면 안 되는 거죠?
-
★백진언 연구원이 개인 사정 때문에 이번 달 말에 피드백을 줄 수 있다고 합니다. 연구원이 올 때까지 친구들끼리 열심히 상의해보자고요!
-
어차피 동전을 미는 건 턴을 돌리는 거죠, 동전1 빈 칸 동전2가 있고 내 턴일 때 동전 2를 잡아야 한다면 빈 칸을 끝까지 밀고 잡아서는 안 된다면 동전 1을 가져갈 것이므로 빈 칸은 몇칸이든 의미가 없습니다. 따라서 빈칸을 한칸으로 통일하고, 동전을 A, 빈 칸을 B라고 한 뒤 은화 앞으로 적당한 A와 B의 나열이 있는 것을 생각합시다. A는 무조건 시행되는 턴이고, B는 B 왼쪽의 A를 잡은 플레이어가 선택할 수 있네요. 은화로부터 시작해서 오른쪽에서 왼쪽으로 턴 순서를 부여할게요. 은화가 0번이니까 최선의 플레이에서 짝수 번째 턴에서 시작하는 사람이 승리합니다. 따라서 시행 여부가 마음대로인 B는 그 앞의 A가 짝수 번째 턴을 부여받게 합니다. 즉 B 오른쪽의 A의 턴 순서가 짝수라면 B는 사용되고(B도 턴 순서를 부여받고) 홀수라면 턴 순서를 부여받지 않습니다. 동전이 배열되어 있을 때 중간에 동전이 없는 모든 빈칸을 B로 치환하고 상기한 한가지의 규칙만 지켜서 은동전으로부터 턴 순서를 부여했을 때, 짝수 동전(혹은 빈칸)에서 시작하는 사람이 승리합니다.
-
'따라서 빈칸을 한칸으로 통일하고' 라는 가정이 조금 이상한 면이 있는 것 같아 말씀드립니다.
빈칸이 두칸이라고 하면 그 빈칸을 아예 없애 버리는 것이 아닌 한칸만 움직이는 것도 가능합니다(문제상황이 그러합니다.).
즉 저렇게 가정한다면 아예 다른 문제가 되어 버리죠.
좋아요0 -
' 내 턴일 때 동전 2를 잡아야 한다면 빈 칸을 끝까지 밀고 잡아서는 안 된다면 동전 1을 가져갈 것이므로 빈 칸은 몇칸이든 의미가 없습니다. '
라고 써두었는데 부족함이 있었던 것 같네요. 빈 칸은 홀짝을 결정하는 기회이므로 몇 칸이 있든 전부 밀어버리거나 동전을 가져와서 자신에게 유리한 쪽으로 결정해야지 그 기회를 상대에게 넘겨주어서는 안됩니다. 빈 칸이 두칸 이상 있을 때 한 칸만 움직이는 것은 최선의 선택이 아닙니다.
좋아요0 -
'우리집고양이'님! 'C'를 그냥 동전, 'S'를 은 동전, 'ㅁ'를 빈칸이라고 할 때 아래 상황에서 첫 플레이어의 필승전략은 맨 오른쪽 동전을 한 칸만 미는 거에요:
ㅁCSㅁㅁC
빈 칸이 두 칸 이상 있을 때 한칸만 움직이는 것도 최선의 선택이 될 수 있습니다
좋아요0 -
문제를 잘못 이해했네요. 감사합니다.
좋아요0
-
-
님게임과 유사한것같네요.
기본적으로 2번시행없이 1번시행으로만 진행한다면
은동전 앞의 동전의 갯수를 p라고 했을때
p가 홀수일때에는 나중에하는 사람이,
짝수일때에는 먼저하는 사람이 이깁니다.
2번시행을 포함해보도록 하겠습니다.
님게임에 비유해, 앞으로 땡길 수 있는 칸 수를 돌의 갯수, 동전의 갯수를 돌무더기의 갯수로 봅니다.
님게임의 경우, 이때 NIM-SUM값이 0이면 나중에하는 사람이, 0이아니면 처음에하는 사람이 이깁니다(타 문제에서 증명되었으므로 생략).
님게임을 이긴다는것은 돌을 전부가져가는것으로 이 게임에서는 더 이상 2번시행을 할 수 없는것과 동일합니다.
즉 NIM-SUM값이 0이면 처음한사람에게 돌아가고, 0이아니면 나중에한사람에게 선이 주어집니다.
종합하면, p값이 짝수이고 NIM-SUM이 0이거나 p값이 홀수이고 NIM-SUM이 0이 아니면 먼저하는 사람이 이깁니다.
-
-
위의 것처럼 하면 맨 처음하는 사람이 동으로 만든 동전을 가져갈 것이고 그러면 두번째로 하는 사람은 선택의 여지가 없으므로 남은 은 동전을 왼쪽으로 한 칸 움직이고 그 다음 가져가면 됩니다.
물론 조건을 구하는 것이기에 별 다른건 도움이 안되지만, 그래도 아이디어를 도출하는데는 도움이 될 듯 합니다.
-
글을 쓰기에 앞서 현재 문제를 간단하게 수로 표현하겠습니다. 0은 빈칸, 1은 동 동전, 2는 은 동전입니다. 예를 들어 0101102101 등의 형식으로 모든 배치를 표현할 수 있습니다. 물론 여기서 2는 반드시 한 번 있어야 하고, 맨 뒷자리는 1 또는 2입니다.(0은 의미가 없기 때문)
현재까지 나온 아이디어를 보면 NIM 게임으로 보고 풀자는 아이디어가 있었는데요, 이것도 하나의 방법이 될 수는 있지만 제 개인적인 생각으로는 좀 복잡해질 것 같습니다.
C언어 님이 제안하신 방법에서의 허점은 A1+A2+•••+An이 같더라도 결과는 다르게 나올 수 있다는 것이고(예를 들어 1002와 012는 값이 5로 같지만 012는 나중에 한 사람이, 1002는 먼저 한 사람이 이깁니다.), code님이 제안하신 방법에서의 허점은 p뿐만 아니라 2 뒤에 있는 배치도 결과에 영향을 준다는 점입니다. 각각 보완할 수는 있긴 한데, 제 생각에는 현재 문제를 NIM게임으로 변환시키면 다음과 같아질 것 같습니다.
(NIM 게임 변환 시 - 모든 동전을 돌 무더기로 표현하되, 은 동전으로 표현되는 돌 무더기에 집중해야 합니다. 각각의 동전을 옮길 수 있는 칸의 수가 각 돌 무더기에 있는 돌의 개수가 되고, 이에 따라 임의의 돌 무더기에 있는 돌의 개수가 k개 줄어들면 그 무더기의 오른쪽에 있는 돌 무더기의 돌 개수는 k개 늘어납니다. 그리고 돌 무더기의 돌 개수가 0개가 되더라도 돌 무더기는 없어지지 않습니다. 맨 왼쪽의 돌 무더기를 없애는 시행을 할 수 있고, 은 동전이 있는 돌 무더기가 맨 왼쪽에 오도록 하는 사람이 패배합니다.)
보시면 알겠지만 현재 게임 방법과 큰 차이가 없기 때문에, NIM게임으로 접근해도 풀이에 별로 도움이 되지 않을 수 있습니다.
저는 위에서 말씀드린 대로 숫자로 표현한 뒤 생각해 보았는데요, 은 동전 앞의 돌의 개수와 은 동전 뒤의 돌의 개수를 기준으로 돌 사이에 빈칸을 넣어보고 있습니다. 아래는 1이 2개일 때까지 제가 알아본 결과입니다. '선'이 먼저 하는 사람이 승리, '후'가 나중에 하는 사람이 승리하는 배치입니다.
[1이 0개]
2 선 / 02 선 / 002 선 •••
[1이 1개]
(1) 12의 형식
12 후 / 102 선 / 1002 선 •••
012 후 / 0102 선 / 01002 선 •••
0012 후 / 00102 선 / 001002 선 •••
••• 후 / ••• 선 / ••• 선 / •••
(2) 21의 형식
항상 '선'이 승리
[1이 2개]
(1) 112의 형식
112 선 / 1102 후 / 11002 선 / 110002 선 •••
1012 선 / 10102 후 / 101002 선 / 1010002 선 •••
10012 선 / 100102 후 / 1001002 선 / 10010002 선 •••
••• 선 / ••• 후 / ••• 선 / ••• 선 / •••
0112 선 / 01102 선 / 011002 후 / 0110002 선 / 01100002 선 •••
01012 선 / 010102 선 / 0101002 후 / 01010002 선 / 010100002 선 •••
010012 선 / 0100102 선 / 01001002 후 / 010010002 선 / 0100100002 선 •••
••• 선 / ••• 선 / ••• 후 / ••• 선 / ••• 선 / •••
a1b1c2(a, b, c는 빈칸)로 표현될 때 c=a+1인 경우에만 '후' 승리
(2) 121의 형식
121 후 / 1201 선 / 12001 선 / •••
1021 후 / 10201 선 / 102001 선 / •••
10021 후 / 100201 선 / 1002001 선 / •••
••• 후 / ••• 선 / ••• 선 / •••
0121 선 / 01201 후 / 012001 선 / 0120001 선 / •••
01021 선 / 010201 후 / 0102001 선 / 01020001 선 / •••
010021 선 / 0100201 후 / 01002001 선 / 010020001 선 / •••
••• 선 / ••• 후 / ••• 선 / ••• 선 / •••
00121 선 / 001201 선 / 0012001 후 / 00120001 선 / 001200001 선 / •••
001021 선 / 0010201 선 / 00102001 후 / 001020001 선 / 0010200001 선 / •••
0010021 선 / 00100201 선 / 001002001 후 / 0010020001 선 / 00100200001 선 / •••
••• 선 / ••• 선 / ••• 후 / ••• 선 / ••• 선 / •••
a1b2c1로 표현될 때 a=c인 경우에만 '후' 승리
(3) 211의 형식
항상 '선'이 승리
위의 결과에서 보듯, 가로줄로 표현되는 배치에서는 후가 딱 한 번 승리하고 그 이후부터는 선이 승리하며, '00100201(선), 001002001(후), 0010020001(선)'의 경우처럼 빈칸의 유무뿐만 아니라 빈칸의 개수도 결과에 영향을 미칩니다.
1의 개수를 늘려가며 규칙을 찾아야겠는데, 이대로만 된다면 문제 해결은 시간 문제겠네요.
아 그리고 칸의 총 개수를 기준으로도 해봤는데, 이건 일반화가 어려워서 동전의 개수로 하는 게 좀 더 편한 것 같습니다.
-
배스킨라빈스 31 게임의 필승 전략처럼 상대의 동작에 따라 수칙을 세우면 될 것 같아요.
처음 하는 사람의 필승 전략
가장 첫번째 동작으로 맨 왼쪽 동전을 가져간다. 다음부터는 상대의 동작에 따라 대응을 달리한다.
1. 상대가 동전을 가져가면 자신도 동전을 가져간다.
2. 상대가 n번째 동전을 왼쪽으로 옮긴다면, 자신은 n+1번째 동전을 n번째 동전의 바로 오른쪽으로 옮긴다.
동전 배치 조건은
1. 은으로 만든 동전은 홀수 번째에 위치한다.
2. 2k번째 동전과 2k+1번째 동전은 항상 이웃한다.(k는 자연수) 예로 2, 3번째 동전은 항상 이웃하며 16,17번째 동전도 항상 이웃한다.
배치와 전략이 다음과 같을 경우 처음 하는 사람은 이기게 됩니다. 왜냐하면, 이 배치에서는 상대방은 항상 짝수 번째 동전만을 조작하고 자신은 항상 홀수 번째 동전만을 조작하기 때문입니다.
-
-
확인요청중
맨 왼쪽부터 동,동,은 동전을 놓으면 될 것 같습니다! 그러면 맨 처음에는 가장 왼쪽에 있는 동 동전을 가져가고, 나중에 하는 사람은 남아있는 동 동전을 가져가거나 동 동전을 왼쪽으로 한 칸 옮길 수밖에 없습니다! 남아있는 동 동전을 가져가는 경우에는 바로 은 동전을 가져가면 되고, 동 동전을 왼쪽으로 한 칸 옮기는 경우에는 은 동전을 왼쪽으로 한 칸 옮깁니다. 그러면 다음 차례에 상대방이 동 동전을 가져갈 수밖에 없기 때문에 그 다음에 제가 은 동전을 가져가면 됩니다!
-
확인요청중
처음하는사람을 A라가정하자, 나중하는사람을 B라고 가정하자
은으로 된 동전과의거리에 관련이있다 1번째 동전부터 n번째 은전까지의거리는 0,a이므로,
거리는 n이다 1번동작은 홀짝성의의해 A는 홀수번째 동전을 가질수있다
그리고 2번째 사람이 옮길때도 생각해야한다. 옮긴다는것은 빈칸이있을때, 턴을 포기한다는 뜻으로 해석이가능하다
턴을포기하면 홀짝성의의해 짝, 홀이 바꿔진다
턴을포기한다는것은 수학적으로 턴-1이기때문에 홀-1 = 짝 짝-1 = 홀이되므로 바뀌어지는것이다
따라서 2번동작은 '패스' 1번은 '추출'로 해석할수있다
빈공간이없을때, 턴포기는 이용할수없다
그러나 한사람이 추출을하면, 왼쪽빈공간이 생기므로 턴포기할수있다
1번주자가 추출만을할수있다. 홀짝, 2번주자의선택권은 추출과 포기 이다 추출할때는 홀짝
포기할때는 짝홀 동전을 홀수에있을때, 이도 홀짝성의의해 홀짝, 짝홀이 바뀌려면, n/2가 짝수가되지않는다. n/2는 홀짝이아니므로A가승리하게된다
-
확인요청중
이 문제의 핵심은 가능한 모든 동전의 배치를 먼저 하는 사람이 이기는 경우와 지는 경우로 나눌 수 있다는 것입니다.
우선 저는 동전의 배치를 전체 동전의 수가 짝수일 때(1번째 동전과 2번째 동전 사이의 거리, 3번째 동전과 4번째 동전 사이의 거리, 5번째 동전과 6번째 동전 사이의 거리, ... , 마지막에서 두번째 동전과 마지막 동전 사이의 거리)로, 전체 동전의 수가 홀수일 때(첫 칸부터 1번째 동전 사이의 거리, 2번째 동전과 3번째 동전 사이의 거리, 4번째 동전과 5번째 동전 사이의 거리, ... , 마지막에서 두번째 동전과 마지막 동전 사이의 거리)로 나타내겠습니다. 예를 들어 은 동전을 2로 표기하는 방법에서 010001102였던 배열은 (3,1)이 되고, 0010120110011은 (2,0,0,0)이 됩니다. 이때 플레이어는 이 수들 중 하나만을 바꿀 수 있는데, 줄이는 쪽으로는 얼마든지 바꿀 수 있고 상대가 늘리는 쪽으로 바꾸면 자신이 원래대로 돌려놓을 수 있으므로 수를 줄이는 경우만 생각하도록 하겠습니다.
1.전체 동전의 수가 짝수이고 은 동전이 짝수번째 동전이거나, 전체 동전의 수가 홀수이고 은 동전이 짝수번째 동전일 때
(0,0,...,0)이 지는 경우이므로 순서에 상관없이 0이 아닌 수의 개수가 2개일 때 그 두 수가 같은 경우는 모두 지는 경우다. 또한 그 개수가 3개일 때는 가장 작은 수가 나머지 두 수의 차고, 어느 두 수도 같지 않은 배열중 앞의 배열과 두 개의 숫자 이상이 곂치지 않는 배열인 (1,2,3), (1,4,5), (1,6,7), (1,8,9),...,(2,4,6),(2,5,7),(2,8,10), (2,9,11),..., (3,5,8), (3,6,9), (3,7,10), (3,11,14),...가 모두 지는 경우이며, 개수가 4개일 때도 이처럼 어느 세 수도 개수가 3개일 때의 지는 경우나 다른 개수가 4개일 때 배열의 지는 경우와 곂치지 않는 배열인 (1,1,2,4), (1,1,3,5), (1,1,6,8), ..., (1,2,5,8), (1,2,6,9), (1,2,7,10), (1,2,11,14),... 등이 모두 지는 경우가 된다. 이 배열들을 살펴보면 가장 큰 수가 나머지 모든 수의 합과 같다는 사실을 알 수 있다. 하지만 가장 큰 수가 나머지 모든 수의 합과 같은 모든 배열이 지는 경우인 것은 아니며, 앞에서 언급한 형태의 모든 경우를 제외한 나머지 모든 경우는 먼저 한 사람이 이기는 경우로, 어느 한 수를 줄여 지는 경우로 만들 수 있다.
2.전체 동전의 수가 짝수이고 은 동전이 홀수번째 동전이거나, 전체 동전의 수가 홀수이고 은 동전이 홀수번째 동전일 때
(0,0,...,0,1)이 지는 경우이므로 첫번째 수만을 특별히 하고, 나머지 수들은 순서에 상관없이 생각하겠다. 이때 첫번째 수를 뺀 배열이 1번의 경우에서 가장 큰 수에 뺐던 첫번째 수를 더한 형태의 배열이 되는 배열이 지는 경우가 되고, 이런 모든 경우를 제외한 나머지 모든 경우는 먼저 한 사람이 이기는 경우로, 어느 한 수를 줄여 지는 경우로 만들 수 있다.
위에서 말한 모든 지는 경우가 아닌 경우이기만 하면 언제나 먼저 하는 사람이 이길 수 있습니다. 왜냐하면 한 숫자를 줄일 때 지는 경우에서 다시 지는 경우로 바꾸는 것은 불가능하지만, 모든 이기는 경우에서는 지는 경우로 바꿀 수 있도록 지는 경우를 설정했기 때문입니다. 즉 필승 전략은 언제나 지는 경우를 상대에게 넘겨주는 것입니다. 이렇게 하면 결과적으로 동전의 개수가 한 단계씩 줄어들어 먼저 한 사람이 은 동전을 가져갈 수 있습니다.
-
확인요청중
저번에 올린 내용으로부터 다시 아이디어를 정리했습니다.
동전의 개수가 홀수일 때는 맨 앞 동전 앞에 있는 빈칸의 수를 중괄호 안에 나타내고, 나머지 동전들을 앞에서부터 두 개씩 묶어 그 두 동전 사이 빈칸의 개수를 순서쌍으로 나타내겠습니다. 예를 들어 010010010002010011은 {1}(2,1,0)입니다.
동전의 개수가 짝수일 때는 동전들을 앞에서부터 두 개씩 묶어 그 두 동전 사이 빈칸의 개수를 순서쌍으로 나타내겠습니다. 예를 들어 0010101001020001001001은 (1,2,3,2)입니다.
이 방법을 썼을 때 동전을 움직여 순서쌍 또는 중괄호의 수 중 하나를 늘리면 다음 사람이 원래대로 돌려 놓을 수 있는데, 이 결과 그 수에 해당하는 두 동전이 앞쪽으로 이동하므로 이런 변환은 유한합니다. 그러므로 이것을 무시하면, 이 게임에서 동전을 움직이는 것은 수 중 하나를 골라 줄이는 것이라고 생각할 수 있습니다. 또한 동전을 가져가는 활동은, 원래 동전이 짝수개였다면 순서쌍의 한 수에 얼마를 더하여 중괄호로 만드는 것이고, 원래 동전이 홀수개였다면 중괄호와 그 안의 수를 삭제하는 것으로 생각할 수 있습니다.
1. 전체 동전의 개수가 짝수일 때
처음 순서쌍의 nim-sum이 0이 되도록 유지시켜 순서쌍의 모든 수를 0으로 만들어야 이길 수 있습니다. 왜냐하면 순서쌍의 모든 수를 0으로 만들면 상대가 동전을 가져가야 하고, 이후 자신도 동전을 가져가면 다시 모두 0이 되어 결과적으로 은 동전도 자신이 가져가기 때문입니다. 이때 은 동전이 홀수번째에 있다면, 상대가 은 동전에서 앞쪽으로 세 번째의 동전을 가져갔을 때 두 번째의 동전을 맨 앞으로 밀면 상대가 그 동전도 가져가게 되고, 자신이 은 동전을 가져갈 수 있습니다. 또한 모두 0이 되기 전 중간에 상대가 동전을 가져간다면 가져갈 때 순서쌍에서 사라진 수에는 1 이상이 추가되어 중괄호로 들어가므로 중괄호 속의 수가 순서쌍의 nim-sum보다 크게 되어 2번에서 말할 지는 형태를 상대가 만들지 못했으므로 자신이 이길 수 있습니다.
2. 전체 동전의 개수가 홀수일 때
순서쌍의 nim-sum이 중괄호의 수보다 1 크도록 유지시키면 이길 수 있습니다. 왜냐하면 이 과정을 반복해서 {0}(0,0,0,...,1,0,...,0)이 되면 상대가 순서쌍을 전부 0으로 만들면 자신이 동전을 가져가서 중괄호를 없애 이길 수 있기 때문입니다. 또 유지시키는 중간에 상대가 동전을 가져간다면 순서쌍의 nim-sum은 변하지 않았으므로 0이 아니어서 자신이 0으로 만듦으로써 이길 수 있습니다.
정리하자면, 먼저 하는 사람이 이길 수 있는 경우는 '은 동전이 맨 앞에 있지 않고 순서쌍의 nim-sum이 0인 경우, 은 동전이 맨 앞에 있지 않고 순서쌍의 nim-sum이 중괄호의 수 +1인 경우' 를 제외한 모든 경우입니다.
-
출제자입니다. 파스칼님이 설명해주신 풀이의 전략이 맞는 전략입니다. 거의 다 푸신 것 같아요! 다만 논리에 보완할 점이 있어 피드백 드려요. 설명을 위해 풀이에서 설명하는 '만들면 무조건 이기는 상태'(전체 동전개수 짝수 -> 순서쌍의 nim sum = 0으로 유지, 전체 동전개수 홀수 -> 중괄호수 + 1 = 순서쌍의 nim sum으로 유지)를 '좋은 상태'라고, 그렇지 않은 상태를 '나쁜 상태'로 부를게요. 보드를 항상 좋은 상태로 유지시킬 수 있으려면, 다음 두가지를 항상 확인되어야 해요.
a. 임의의 나쁜 상태는 어떤 움직임을 하면 항상 좋은 상태로 만들 수 있는가?
b. 임의의 좋은 상태는 어떻게 움직여도 무조건 나쁜 상태인가?
만약 a가 사실이 아니라면 내가 어떤 움직임을 해도 좋은 상태로 못 만드는 나쁜 상태를 상대가 내게 넘길 수 있고, b가 사실이 아니라면 상대가 좋은 상태를 받아도 역으로 내게 좋은 상태를 만들어 넘겨줄 수 있겠죠. 반대로 a와 b를 확인하면 필승 전략이 됨도 생각해보면 알 수 있어요. 만약 NIM 게임을 공부하셨다면 NIM 게임 전략도 a와 b를 확인하는 식으로 증명한다는 걸 알 수 있을 거에요. 파스칼님의 풀이에서는 2번 경우에서 중괄호가 들어가는 것 때문에 NIM게임과 조건이 약간 달라져 a와 b를 새로 확인해줘야 해요. 그러니까, 왜 하필 순서쌍의 nim-sum이 중괄호의 수보다 딱 1이 커야 하는지가 a와 b를 보이는 데 써져야겠죠? 궁금한 점이 있으시거나 해결하셨으면 대댓글로 확인해드릴게요!
좋아요0
-
-
해결
출제자님의 의견에 따라 논리를 보충하도록 하겠습니다.
2번 경우인 '동전의 개수가 홀수일 때', b, 즉 좋은 상태에서는 나쁜 상태밖에 만들 수 없음을 먼저 보이겠습니다.
상대가 동전을 가져가는 경우는 이미 증명했으므로 동전을 움직이는 경우만 증명하면 됩니다. 상대가 동전을 움직이는 경우는 중괄호의 수를 줄이는 경우와 순서쌍 속 수를 줄이는 경우로 나눌 수 있습니다. 상대가 중괄호를 줄이면, 순서쌍의 nim-sum에는 변화가 없으므로 중괄호의 수보다 순서쌍의 nim-sum이 1 큰 상태를 유지시킬 수 없습니다. 또한 상대가 순서쌍 속의 한 수를 줄이면, 상대가 줄인 수를 제외한 나머지 수들의 nim-sum이 상대가 줄인 수의 원래 값과 중괄호 속 수+1을 xor 연산한 값과 같으므로, 상대가 줄인 후에는 이 값이 달라져서 순서쌍의 nim-sum이 중괄호의 수보다 1 큰 상태가 유지될 수 없습니다.
이번에는 a, 즉 나쁜 상태에서 언제나 좋은 상태를 만들 수 있음을 보이겠습니다.
나쁜 상태이므로 순서쌍의 nim-sum이 중괄호의 수+1보다 작은 상태와 큰 상태로 나눌 수 있습니다. 만약 작은 상태라면, 중괄호의 수를 줄임으로써 중괄호의 수 +1이 순서쌍의 nim-sum과 같도록 만들 수 있습니다. 이때 만약 nim-sum이 0이라면 동전을 가져가 중괄호를 없앰으로써 동전이 짝수일 때의 이기는 경우로 만들 수 있습니다. 만약 nim-sum이 중괄호의 수+1보다 큰 상태라면, nim-sum 의 수와 중괄호 속 수+1을 각각 이진수로 나타냈을 때, 자릿수가 서로 다른 가장 높은 자리에 대해 nim-sum의 자릿수가 1, 중괄호 속 수 +1의 자릿수가 0이어야 합니다. 이것은 순서쌍 안의 수 중 해당하는 자리가 1인 수가 적어도 하나는 있음을 의미하고, 그 수의 해당하는 자리를 0으로 낮추면 그 아래 자릿수들을 어떻게 조작해도 순서쌍 속 그 수를 줄인 것이 되므로 나쁜 상태를 받았을 때 좋은 상태로 넘겨주는 것이 항상 가능합니다.
위와 같이 a, b를 모두 증명했습니다.