폴리매스

1) 삼목의 필승법칙은 먼저 하는 사람이 무조건 승리합니다.

취미로 해 본 사람은 알겠지만(...)

 

먼저 하는 사람이 적당한 칸 A에 놓고(적당한 칸은 아래 댓글 참조) 상대가 B로 막으면,

A 옆에는 여덟 칸이 있는데, 그 칸들 중 B와 B를 A에 점대칭 이동한 점을 제외하고 아무 곳에나 놓으면 뚫린 2가 만들어집니다.

이제 상대가 어느 곳을 막아도 무조건 이길 수 있습니다.

검은 돌이 선공이라고 하면 

      

     ●

     

이렇게 놓을 자리가 생기는데

그 다음 흰 돌이

        ○

 ●

 

이렇게 놓으면

검은 색 돌을 

        ○

●     ●

놓고

흰 색 돌이 검은 돌 옆에 두지 않으면 검은색이 뻥 뚤린 3개의 연속으로 이길 수 있고

 

       ○

●    ●    ○

 

이렇게 놓으면

 

●

 ※    ○

●    ●    ○

 

이렇게 놓고 

 

흰 돌이 ※ 위치에 놓지 않으면 

검은 돌을 ※ 위치에 놓아 이기고

흰 돌을 ※ 위치에 놓았다면

 

         ●

  ☆    ○    ○

         ●    ●    ○

 

검은 돌을 ☆ 위치에 놓아 주변에 아무것도 없는 쌍 2개가 되어 무조건 이길수 있는 필승 전략이 탄생하지 않나요?

 

다른 모양은 모두 각각 45k^o 만큼 돌려서 모두 만들 수 있다고 생각합니다

 

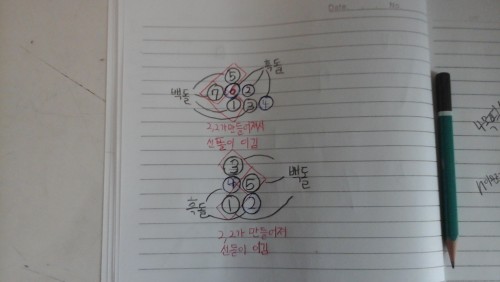
이렇게 4목의 필승조건은 선공이 2번째에 둔 상대의 위치를 보고 위의 사진처럼만 대응한다면 전개는 상대는 어쩔수 없이 위의 사진과 같이 대응할수 밖에 없습니다.

n목을 각 선수가 최선의 수를 두며 진행한다고 할때, (n-2)의 양쪽 다 뚫린 모양을 두 개 이상 만들 수 있으면 이길 수 있습니다. 두 개 이상의 뚫린 (n-2)모양을 만드려면 1)하나의 (n-2)모양과 두 개 이상의 (n-3)모양(단, 서로 이어 두 개 이상의 (n-2)모양을 만들 수 있어야 함. ex)대각선 연결)을 만들어야 하죠. 4목까지는 쉽습니다. 그냥 한 수를 놓기만 해도 (n-3)모양이 되고, 한 방향이 막혀도 한 점에서 뻗을 수 있는 방향은 8방향이니 문제 없이 (n-2)모양, 이걸 막으면 대각선 방향 (n-2)모양을 만들고 이것 또한 막으면 다시 하나를 놔서 두 개의 (n-2)모양을 만들어 승리할 수 있습니다(후플을 막아야겠지만 적당히 하면 되는 수가 있을거라 생각됩니다.). 반면 오목은 (n-2)모양 두 개(흔히 삼삼이라고 하죠. 규칙으로 제한하기도 하지만 일단 가능하다고 합니다.)를 만들어야 하는데, 이를 만들기까지 상대 선수의 방해가 만만치 않을 것 같습니다. 확실히 4-3-3모양을 만들어야 하는 육목에는 필승전략이 없고, 최선의 수를 두면 무승부로 갈 것 같습니다. 오목도 마찬가지일 것 같기는 한데, 마스터 수준의 선수가 고모쿠룰(모든 모양 허용)로 진행하면 선플이 무조건 유리하다고 하니 아닌것도 같네요. 역추적으로 잘 찾아보면 답이 나오지 않을까 생각해 봅니다.

오목의 필승법칙은 존재하지 않는 것 같습니다.. 오목을 해보면 아는데 오목은 3x1이 2개 만들어지거나 4x1 이 만들어져야 한다. 고로 오목의 필승법칙은 없다.

오목을 해봐서 아는데 흑은  반3^.3,반3^.4,반4^.4,6,3^.3,4^.4 를 둘 수 없습니다

백도 4^.4,6 을 둘 수 없습니다.

^.

3목은 내 차례일 때 막히지 않은 2를 만들면 승리하고

4목은 내 차례일 때 막히지 않은 3을 만들면 승리하며

5목은 내 차례일때 막히지 않은 4를 만들면 승리합니다.

즉, 3목에서 33법칙이 적용된다면 3목에서는 흑돌이 돌을 둘 수 없으므로 백돌이 승리하고, 4목은 흑이 22를 만들지 못하므로 금수유도로 백돌이 승리할 가능성이 높으며 (떨어진 33이 가능한 경우에는 흑돌이 승리할 가능성이 높다)

5목은 서로 최선의 수를 둔다면 무승부가 될 것이라고 생각합니다.

하지만 33을 허용할 경우엔 흑돌이 무조건 승리할 수 있을 것이라고 생각 합니다.

n목의 경우 무조건 승리하는 수따위는 없습니다.