기사 작성법

좋은 기사를 쓰려면 어떻게 해야 할까요?

매스포터 여러분 안녕하세요!
'기사'라고 하니 거창해 보이지만, 기사는 형태가 다른 하나의 글이랍니다. 기사라고 반드시 신문에서 보는 기사 형태일 필요는 없습니다. 수학동아의 다양한 기사를 보고 자유로운 형식으로 써주세요! 본격적으로 기사를 쓰기 앞서 좋은 기사를 쓰기 위한 몇 가지 '꿀팁'을 알려 드릴게요. 이것만 지켜도 훌륭한 기사를 쓸 수 있답니다!

01 제목 정하기

기사를 볼 때 가장 먼저 보는 게 무엇인가요? 바로 제목입니다. 아무리 잘 쓴 기사라도 제목이 재미없으면 눈길이 안 가기 마련입니다. 기사의 제목은 기사의 주제를 담고 있으면서도 사람들의 흥미를 끌 수 있어야 합니다.
02 육하원칙 지키기

도형의 기본 요소가 점, 선, 면인 것처럼 문장의 기본 요소는 '육하원칙(언제, 누가, 어디서, 무엇을, 어떻게, 왜)'입니다. 육하원칙을 잘 지킨 문장은 명확하고 많은 정보를 담고 있기 때문에 이해하기가 쉽습니다.
03 띄어쓰기와 맞춤법 지키기

기사의 목적은 새로운 정보를 정확하게 전달하는 것입니다. 그런데 기사에 띄어쓰기나 맞춤법이 잘못돼 있으면 신뢰하기 어렵겠죠? 기사를 다 쓰고 잘못 쓴 단어나 문장은 없는지 한 번 더 확인해주세요.
04 문장은 짧게, 다양한 단어 이용하기

한 번에 읽기 편하도록 문장은 짧게 써주세요. 문장이 길어지면 주어와 서술어가 맞지 않거나, 같은 말을 반복하는 등의 실수를 하기 쉬워요. 문장을 줄이고 싶으면 '굉장히', '매우'와 같은 미사여구나 '그런데', '따라서'와 같은 접속사 중 불필요한 표현을 빼주세요. 또 한 문장에서 같은 단어가 되풀이되지 않게 다양한 단어를 이용해보세요. 글이 훨씬 풍성해 질 거예요.
05 사진 또는 그림 설명하기

기사 내용과 관련 있는 사진과 그림에 대한 설명을 꼭 달아주세요! 기사의 내용을 이해하는 데 큰 도움이 된답니다. 이때 본인이 직접 찍은 사진만 사용해 주세요. 포털 사이트에서 허락없이 가져오는 사진이나 그림은 저작권에 문제가 될 수 있습니다. 저작권에 문제가 없는 사진일 경우 꼭 출처를 밝혀주세요!
Plus + 재미있는 퀴즈 내기

매스포터에서는 기사의 마지막에 기사 내용과 관련 있는 퀴즈를 내야 합니다. 퀴즈를 통해 기사를 읽는 사람들이 내용을 한층 더 깊게 이해할 수 있을 거예요!

위의 사항을 제대로 지키지 않은 기사는 홈페이지에 보이지 않을 수 있으니, 꼭 ‘기사작성법’을 숙지하고 기사를 작성해주세요

[개념 기사] 위대하신 고라스 형님의 정리에서의 성질

Dr.K 2021.02.28 20:33

페이스북 트위터 카카오톡 카카오스토리 네이버블로그 네이버밴드

기원전 사람이었던 피타고라스는 피타고라스학파를 만들어 여러가지 토론하고 수에 대해 엄청난 생각을 가지고 있는 사람이었다. 피타고라스는 만물의 근원이 '수' 라고 생각한 독득한 인물이였다. 그래서 1은 모든 수의 본질 이고 2는 여성, 3은 남성 2+3인 5는 결혼이라고 생각하였다.

피타고라스의 업적은 10개도 넘는다. 1 홀수와 짝수의 분류 2 사각수와 삼각수 3 홀수의 합과 사각수의 관계 4 완전수의 발견 5 친화수의 발견 6 무리수의 발견 7 삼각형의 내각의 합은 2×직각임 8 황금분할 9 정삼각형의 작도 10 정다면체는 5종류임을 증명 ... 등이 있다. 하지만 그중에서 피타고라스 정리가 가장 업적 중에서 대표라고 할 수 있다.

피타고라스의 정리란 직각삼각형의 3개의 변을 a,b,c,라고 하고 c에 대한 각이 직각일 때 a² +b² =c² 이 됨을 뜻하는 것으로서, 고대 그리스의 피타고라스가 증명했다고 하여 피타고라스의 정리라고 불리운다. 피타고라스는 이것뿐만 아니라 다양한 성질을 담고 있다. 삼각형 ABC 에서 각 A=90°, 선분 AD가 선분 BC와 수직 일때

c²= ax b²= ay h²= xy bc= ah 이다.

이러한 성질이 나오는 이유를 증명해 보면

삼각형 ABC가 삼각형 DBA와 닮음이다. 선분 AB : 선분 DB= 선분 BC : 선분 BA 이므로 선분 BA2 = 선분 BD×선분 BC 이다. 따라서 C²=ax

삼각형 ABC가 삼각형 DAC와 닮음이다. 선분 BC : 선분 AC= 선분 AC : 선분 DC 이므로 선분 AC2 = 선분 CD×선분 CB 이다. 따라서 B² =ay

삼각형 DBA가 삼각형 DAC와 닮음이다. 선분 BD : 선분 AD = 선분 AD : 선분 CD 이므로 선분 AC2 = 선분 BC×선분 DC 이다. 따라서 H² =xy

직각삼각형 ABC의 넓이는 1/2 ×선분 AB×선분 AC =1/2×선분BC×선분 AD 이므로 bc=ah

그외에도

직각삼각형 ABC에서 직각을 낀 두변을 지름으로 하는 반원의 넓이를 각각 S_1,S₂라고 하고, 빗변을 지름으로 하는 반원의 넓이를 S₃라고 할 때, S₁+S₂=S₃이다.

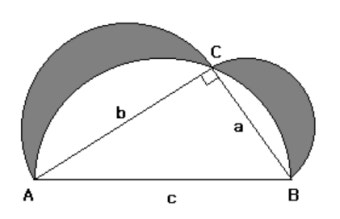
또한 히포크라테스의 원의 넓이도 있는데 직각삼각형 ABC의 세 변을 지름으로 하는 세 반원에서 색칠한 부분의 넓이는 1/2bc가 된다.

피타고라스의 정리는 옛날부터 오늘날까지 많은 관심사이다. 동양의 피타고라스의 정리라고 불리우는 구고현의 정리가 아시아에서 발견되었고 많은 수학자에서 미국 대통령까지 피타고라스의 정리를 증명했다고 한다.

기사를 끝 마치며 퀴즈!

직각삼각형에서 빗변이 29 높이가 21일때 밑변의 넓이는 얼마 일까?

태그

#피타고라스정리 #히포크라테스의원의넓이

A PHP Error was encountered

Severity: Warning

Message: Undefined variable $tag_news_list

Filename: inc/article_view.php

Line Number: 90

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/article_view.php
Line: 90
Function: _error_handler

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Article.php
Line: 221
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: Warning

Message: Cannot modify header information - headers already sent by (output started at /volume1/web/PhpstormProjects/www_polymath_co_kr/system/core/Exceptions.php:271)

Filename: core/Common.php

Line Number: 570

Backtrace:

An uncaught Exception was encountered

Type: TypeError

Message: count(): Argument #1 ($value) must be of type Countable|array, null given

Filename: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/article_view.php

Line Number: 90

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Article.php
Line: 221
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once