여러분은 피보나치 수열에 대해 아시나요?

피보나치 수열은 이탈리아의 수학자 레오나르도 피보나치가 고안한 수열이에요.

(레오나르도 피보나치, 출처 : 위키백과)

수열의 점화식은 아래와 같습니다.

fibo_i = fibo_i-1 + fibo_i-2

초항은 fibo₁=0, fibo₂=1 이라고 표기하기도 하고, fibo₁=1, fibo₂=1 이라고 하기도 해요.

이 기사에서는 후자로 고려하여 쓰겠습니다.

이 점화식으로 피보나치 수열을 10번째 항까지 구해보면 아래와 같습니다.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55.

언뜻 보면 평범한 수열처럼 보일 수 있는데요.

지금부터 이 수열에 숨겨진 굉장한 비밀들을 소개해 드리겠습니다!

첫번째로, i>1인 정수 i에 대하여 fibo_i ÷ fibo_i-1 을 계산해볼게요.

1, 2, 1.5, 1.666..., 1.6, 1.625, ...

어떤 수가 떠오르시나요?

아마 황금비인 1 : 1.618... 에서의 1.618 과 비슷하다는 것을 발견하실 수 있을 거에요.

비교적 작은 수들로 계산하여 실제 황금비율과 차이가 다소 있는 것을 알 수 있는데요.

점차 큰 피보나치 수열의 원소로 계산하면 값이 황금비율에 근접하게 됩니다.

두번째로, 피보나치 수열은 자연에서 쉽게 나타납니다.

대체로 꽃잎의 수에서 잘 나타나는데요.

백합의 꽃잎은 3장, 채송화나 장미는 5장, 코스모스는 8장입니다.

또, 금잔화는 13장, 치커리는 21장, 데이지는 34장, 쑥부쟁이는 55장 혹은 89장의 꽃잎을 가진다고 해요.

잘 살펴보면, 전부 피보나치 수열에 있었던 수들입니다.

89는 피보나치 수열에서 11번째 항이에요.

그런데, 왜 꽃들은 피보나치 수열을 따를까요?

꽃은 피기 전에는 암술과 수술을 잘 보호해야 하고, 핀 후에는 햇빛을 골고루 잘 받을 수 있어야 해요.

효율적으로 이 두가지를 모두 만족할 수 있는 꽃잎의 수가 바로 피보나치 수열의 항들이라고 한답니다.

마지막으로, 정말 재미있는 성질이 하나 더 있는데요.

여러분은 아래와 같은 문제를 본 적이 있을 겁니다.

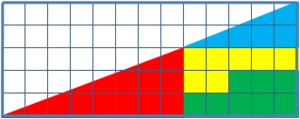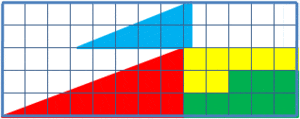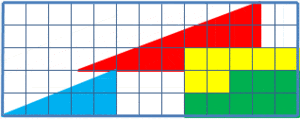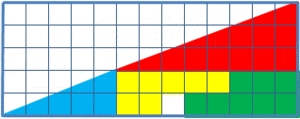
(출처 : 위키피디아)

바로, 사라진 하나의 정사각형에 대한 문제인데요!

자세히 보신 분들은 아시겠지만, 이 속임수는 대각선에 미세하게 변화가 생긴다는 거에요.

중간에 하나의 빈 단위 정사각형이 생기면서 대각선이 약간 더 볼록해지는데요.

이를 gif로 보여주거나 두 개의 그림으로 나누어 보여주면 거의 차이가 없다고 느껴 착각하기 쉽다고 해요.

이 속임수와 피보나치 수열이 무슨 관련이냐고요?

지금부터 설명해드리겠습니다!

위 gif에서 직사각형의 양 변의 길이는 얼마인가요?

정말 신기하게도 5와 13입니다.

그렇기 때문에 총 직사각형의 넓이는 5×13=65인데요.

사라진 하나의 정사각형 때문에 이 직사각형의 넓이가 64 이라고 하기도 합니다.

이렇게 64=65 이라는 하나의 속임수를 만드는 것이죠.

64를 잘 보면 8²입니다.

64와 65에서 찾은 수들을 보면 각각 5, 8, 13인데요.

이는 연속한 3개의 피보나치 수열의 항입니다!

비슷한 원리로 8×21 직사각형과 한 변의 길이가 13인 정사각형으로도 같은 속임수를 사용할 수 있어요.

세 수의 크기가 커지면 커질수록 대각선의 변화를 알아채기 어렵답니다.

-------------------------

이렇게 피보나치 수열에 숨어있는 3가지 비밀을 소개해드렸는데요!

저는 마지막 비밀이 가장 신기했던 것 같습니다.

여러분은 어떤 특징이 제일 신기했었나요?

위에 소개한 비밀 외에도 아는 피보나치 수열의 특징이 있다면 댓글에 공유해주세요!

-------------------------

오늘의 퀴즈!

꽃잎의 수 외에 자연에서 찾을 수 있는 피보나치 수열은 어디에 있을까요?

또한, 이 경우 왜 개수가 피보나치 수열을 따를지도 고민해봅시다.

-------------------------