자유 기사 기사 작성법

일상생활 속 수학을 찾아 보세요!

기사 작성법

좋은 기사를 쓰려면 어떻게 해야 할까요?

매스포터 여러분 안녕하세요!
'기사'라고 하니 거창해 보이지만, 기사는 형태가 다른 하나의 글이랍니다. 기사라고 반드시 신문에서 보는 기사 형태일 필요는 없습니다. 수학동아의 다양한 기사를 보고 자유로운 형식으로 써주세요! 본격적으로 기사를 쓰기 앞서 좋은 기사를 쓰기 위한 몇 가지 '꿀팁'을 알려 드릴게요. 이것만 지켜도 훌륭한 기사를 쓸 수 있답니다!

01 제목 정하기

기사를 볼 때 가장 먼저 보는 게 무엇인가요? 바로 제목입니다. 아무리 잘 쓴 기사라도 제목이 재미없으면 눈길이 안 가기 마련입니다. 기사의 제목은 기사의 주제를 담고 있으면서도 사람들의 흥미를 끌 수 있어야 합니다.
02 육하원칙 지키기

도형의 기본 요소가 점, 선, 면인 것처럼 문장의 기본 요소는 '육하원칙(언제, 누가, 어디서, 무엇을, 어떻게, 왜)'입니다. 육하원칙을 잘 지킨 문장은 명확하고 많은 정보를 담고 있기 때문에 이해하기가 쉽습니다.
03 띄어쓰기와 맞춤법 지키기

기사의 목적은 새로운 정보를 정확하게 전달하는 것입니다. 그런데 기사에 띄어쓰기나 맞춤법이 잘못돼 있으면 신뢰하기 어렵겠죠? 기사를 다 쓰고 잘못 쓴 단어나 문장은 없는지 한 번 더 확인해주세요.
04 문장은 짧게, 다양한 단어 이용하기

한 번에 읽기 편하도록 문장은 짧게 써주세요. 문장이 길어지면 주어와 서술어가 맞지 않거나, 같은 말을 반복하는 등의 실수를 하기 쉬워요. 문장을 줄이고 싶으면 '굉장히', '매우'와 같은 미사여구나 '그런데', '따라서'와 같은 접속사 중 불필요한 표현을 빼주세요. 또 한 문장에서 같은 단어가 되풀이되지 않게 다양한 단어를 이용해보세요. 글이 훨씬 풍성해 질 거예요.
05 사진 또는 그림 설명하기

기사 내용과 관련 있는 사진과 그림에 대한 설명을 꼭 달아주세요! 기사의 내용을 이해하는 데 큰 도움이 된답니다. 이때 본인이 직접 찍은 사진만 사용해 주세요. 포털 사이트에서 허락없이 가져오는 사진이나 그림은 저작권에 문제가 될 수 있습니다. 저작권에 문제가 없는 사진일 경우 꼭 출처를 밝혀주세요!
Plus + 재미있는 퀴즈 내기

매스포터에서는 기사의 마지막에 기사 내용과 관련 있는 퀴즈를 내야 합니다. 퀴즈를 통해 기사를 읽는 사람들이 내용을 한층 더 깊게 이해할 수 있을 거예요!

위의 사항을 제대로 지키지 않은 기사는 홈페이지에 보이지 않을 수 있으니, 꼭 ‘기사작성법’을 숙지하고 기사를 작성해주세요

[자유 기사] 주판 속에서 수학을 찾아보자!

space 2020.09.18 04:14

페이스북 트위터 카카오톡 카카오스토리 네이버블로그 네이버밴드

주판은 계산할 때 쓰는 기구이다. 수판, 산판, 셈 판이라고도 표현한다. 주판을 사용하여 계산하는 것을 주산이라고 하는데 이것을 '놓는다'고도 표현한다.

오래 전인 기원전 2700~2300년, 수메르에서 주판이 사용되었다. 그리고 주판은 그리스와 로마를 경유하여 명나라 이후에 중국으로 전래되었고 개량되었는데, 우리가 아는 주판의 모습은 중국의 모습이다. 한반도에는 조선 초기에 들어왔지만, 일부 상인들 외에 그다지 널리 쓰이지는 못했다.

왜냐하면, 우리나라에서는 훨씬 이전에 중국에서 들어온 산가지를 사용한 계산이 크게 발전했기 때문이다. 정작 중국 대륙에서는 명나라 때부터 상업에 필요한 실용수학계산 위주로 수학이 발전했다. 주판이 알려지고 개량되어 보급된 이후 산가지가 사라졌으나, 한반도에서는 여전히 산가지를 사용한 수학계산을 선호하였다. 더불어 방정식과 제곱근 풀이 역시 중국에보다 한반도에서 더욱 깊이 연구되었다. 이 때문에 청나라 때 청나라의 조정을 방문한 조선 사신들이 서양식 수학 계산법이 필요한 피타고라스 함수를 제외한 모든 높은 난이도의 수학문제들을 산가지로 척척 풀어버리자 청나라 조정의 대신들이 크게 놀라기도 했다.

1970년대에 전자계산기가 보급되기 전까지만 해도 계산을 하는 데에 있어서 필수적인 물건이었고, 보급 초기에는 계산기가 맞는지 틀리는지 주판으로 검산하거나 보조하는 경우도 있었다. 주판을 접하지 않고 자란 요즘 세대들에게도 원리 자체는 익숙한 물건이다. 그리고 덧셈, 뺄셈만 가능할 거라 생각하기 쉽지만, 곱셈과 나눗셈도 할 수 있다. 현대에 쓰이는 개량형을 기준으로, 기준점(소수 첫째자리)의 우측 1/3 가량의 주판알들이 바로 곱셈과 나눗셈을 위한 영역이다.

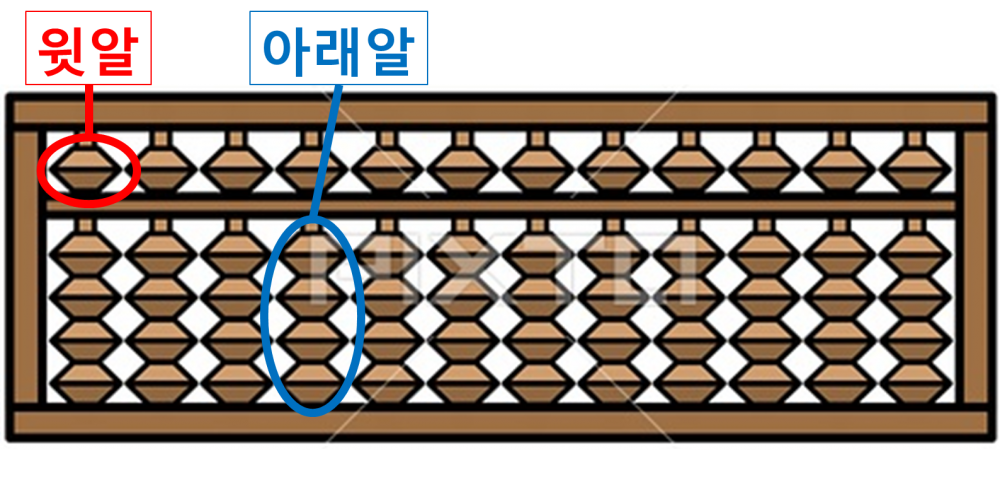
주판의 사용법은 주판의 윗알은 5에 대응하며 검지로 움직이고, 윗알은 내려와 있을 때 +5가 된 것으로 간주한다. 또한 아래알은 값이 1개당 1에 대응하는 알로 엄지로 움직이며, 아래알은 올라와 있을 때 그 수만큼 더해주는 것이다.

또 각자리 수마다 자리수값을 곱해준다

x와 합쳐서 10이 되는 수 y를 10의 보수라 한다. x+y=10이라면 x는 y의 y는 x의 보수 관계가 성립하는 것이다. 1↔9 2↔8 3↔7 4↔6 5↔5 10의 보수는 자릿수의 올림을 효과적으로 처리하기 위한 것이니 주산을 익히고자 하면 이것을 무조건 익혀야 한다. 또한, x와 합쳐서 5가 되는 수 y를 5의 짝이라 한다. 우리가 흔히 말하는 2의 배수 짝수라는 관계없는 말로 x+y=5라면 x는 y의 y는 x의 5의 짝 관계가 성립하는 것이다. 1↔4 2↔3 5의 짝은 같은 자리 내에서 윗알을 이용해서 알이 부족한 경우를 효과적으로 처리하기 위한 방법이니 이것 또한 알아둬야 한다.

덧셈 값에 맞게 아래알을 올리고 위알을 내리되, 알의 수가 모자라 더 이상 계산이 진행되지 않을 땐 보수를 이용하여 해결한다(다음 자리의 아래알 하나를 올린 후, 기존 자리에선 더해야 할 수의 보수만큼 빼준다). 경우에 따라서는 짝도 이용한다. 예를 들어, 24+18을 주산으로 할 시, 먼저 십의 자리에서 2+1→3을 한 후, 일의 자리에서 4+8을 하려는 데, 12이므로 알 수가 모자란 것을 볼 수 있다. 이런 경우 2+1→3까지의 계산이 완료됐으면 십의 자리에서 알 1개를 올려 3+1→4를 먼저 해준 후, 4+8에서 8의 보수인 2만큼을 4에서 덜어내준다. 4-2→2 이리하여 42

뺄셈

받아 올림이 있는 덧셈을 거꾸로 계산하는 것과 같다. 값에 맞게 아래알을 내리고 위알을 올리되, 알의 수가 모자라 더 이상 계산이 진행되지 않을 땐 보수를 이용하여 해결한다(다음 자리의 아래알 하나를 내린 후, 기존 자리에선 빼야 할 수의 보수만큼 더해준다). 경우에 따라서는 짝도 이용한다. 예를 들어, 53-27을 주산으로 할 시, 5-2인 데, 계산에 사용할 아래알이 없다. 이럴 땐, 윗알을 올려준 후, 2의 짝수 3을 더해준다. 십의 자리 수가 3이 된 후, 일의 자리수 3-7을 하려니 또 1자리 알의 수가 부족하다. 이럴 땐 십의 자리에서 알 1개를 내려 3-1→2를 먼저 해준 후, 3-7에서 7의 보수인 3만큼을 더해준다. 근데 또 알이 모자라니 일의 자리에서 윗알을 내려준 후, 3의 짝수인 2만큼 빼준다. 따라서 26이다.

곱셈

곱셈을 할 때는, 자릿수를 잡는 것이 먼저다. 이를 하려면 구구단을 이용하게 된다.

또한 구구단의 모든 경우에서 두자리 수 이하만 나오는 것을 생각하는 것이 필요하다. 즉, 주산에서는 2X4=8 보단 08로 연상하는 것이 필요하다. x자리 수와 y자리 수 를 계산하려면 x+y 자리수에서 곱셈을 시작한다. 예를 들어, 19X43을 주산으로 할 시, 19는 2자리 수 43은 2자리 수 이므로 2+2→4자리수에서 곱셈을 시작한다. 1(2자리)X4(2자리)→04이므로 4번째에 0 3번째에 4를 놓는다. 9(1자리)X4(2자리)→36이므로 3번째에 3 2번째에 6을 놓는다. 1(2자리)X3(1자리)→03이므로 3번째 자리에 0 두번째 자리에 3을 놓는다. 9(1자리)X3(1자리)→27이므로 두번째 자리에 2 첫번째 자리에 7을 놓는다. 위 결과들을 모아놓으면 0400+0360+0030+0027이다. 나머지 계산들은 덧셈때와 같다. 결과는 817이다.

나눗셈

나눗셈을 할 때도 곱셈처럼 자릿수를 잡는 것이 먼저다. 다만 이번엔 손이 아니라 알이 이 위치로 간다. 주판에서 점이 있는 부분의 자릿수를 1로 잡고, 좌로는 1씩 커지고 우로는 1씩 작아진다.

x자리 수와 y자리 수를 계산하려면 x-y-1자리에서 알을 놓는다. 그 후, x와 y의 가장 앞 자리 수를 비교해서, x가 크면 한 칸 건너서, y가 크면 바로 그 앞에서 계산을 시작한다. 예를 들어, 682÷22를 할 시, 682는 3자리 수 22는 2자리 수 이므로 3-2-1→0자리수에 놓는다. 6은 2보다 크므로 한 칸 건너서 십의 자리에서부터 계산을 시작한다. 68은 22가 3번 들어가므로 3을 십에 자리에 놓고 66만큼 덜어준다. 682-660→22 22에는 22가 1번 들어가므로 일의 자리에는 1을 놓고 22를 빼준다. 결과는 31 옛부터 내려오는 주산의 나눗셈 계산법으로 귀제법과 그에 연관된 별도의 구구단이 존재하나, 이미 1970년대 거의 자취를 감추고 대부분 위의 방법을 사용했다. 위와 같이 일반적인 구구단을 이용하는 주산의 곱셉과 나눗셈을 상제법이라고 부른다.

오늘의 퀴즈!

주판 속에 있는 알이 아닌 것은?(2개)

1.윗알

2.중간알

3.아래알

4.타조알

정답을 비밀 댓글로 남겨주세요

첫 기사이니 부족하더라도 봐주세요!

태그

#주판 #옛날 #중국

A PHP Error was encountered

Severity: Warning

Message: Undefined variable $tag_news_list

Filename: inc/article_view.php

Line Number: 90

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/article_view.php
Line: 90
Function: _error_handler

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Article.php
Line: 221
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once

A PHP Error was encountered

Severity: Warning

Message: Cannot modify header information - headers already sent by (output started at /volume1/web/PhpstormProjects/www_polymath_co_kr/system/core/Exceptions.php:271)

Filename: core/Common.php

Line Number: 570

Backtrace:

An uncaught Exception was encountered

Type: TypeError

Message: count(): Argument #1 ($value) must be of type Countable|array, null given

Filename: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/views/ver3/inc/article_view.php

Line Number: 90

Backtrace:

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/application/controllers/ver3/Article.php
Line: 221
Function: view

File: /volume1/web/PhpstormProjects/www_polymath_co_kr/index.php
Line: 315
Function: require_once